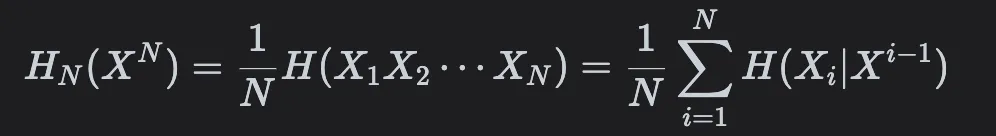CH3-离散和连续源的信息熵

• [Chain rules for Entropy]
  • 计算有记忆源的信息熵公式.
• [带记忆多符号离散平稳源的极限熵]
  • 定义为:
  • 
    • 平均符号熵和条件熵都会趋于稳定值（极限熵）.
      • [?]

连续熵

• [微分熵]
  • 这是去掉无穷大项以后的相对熵.
  • 计算机内部先离散.
• [正态分布熵]
  • 逆天，我推的. 注意积 时，令 :

• 最大熵定理
  • 同样方差情况下，正态分布熵最大.
• : 符号等概率分布情况下具有的熵.
• 利用率 , 冗余度
• 信源编码：冗余度越小越好
  • 信道编码：需要增加一些冗余度以提升抗干扰性.

杂项

• 条件熵一定小于无条件熵