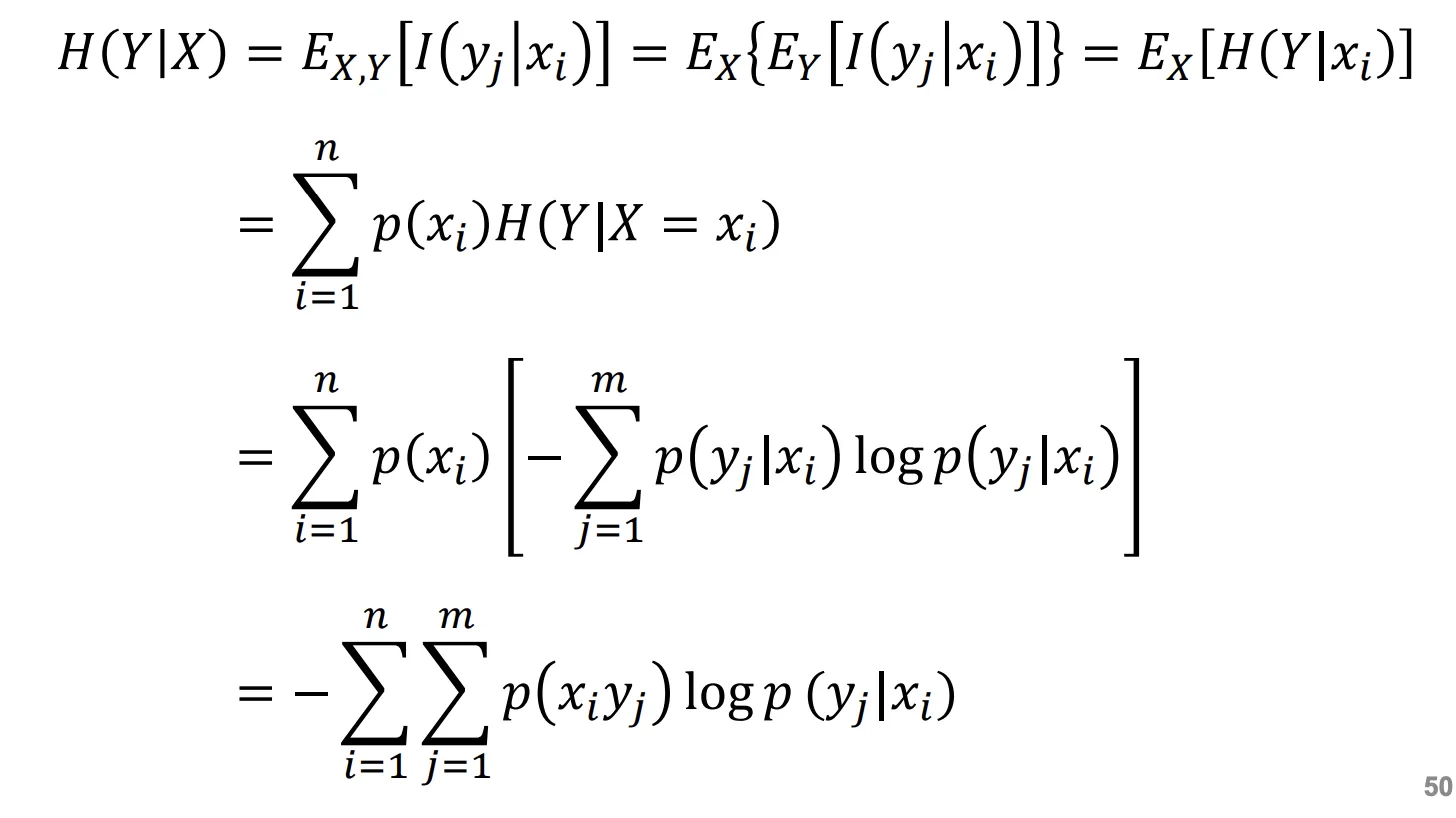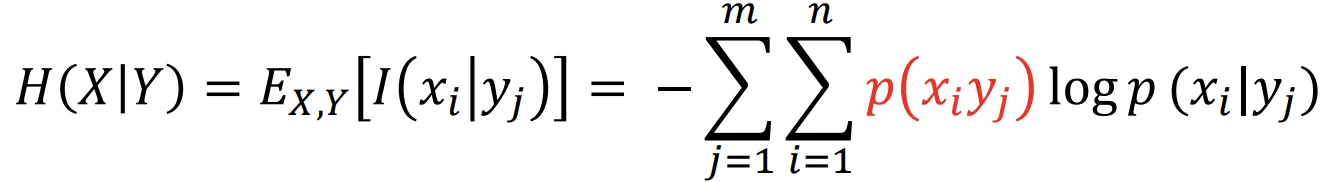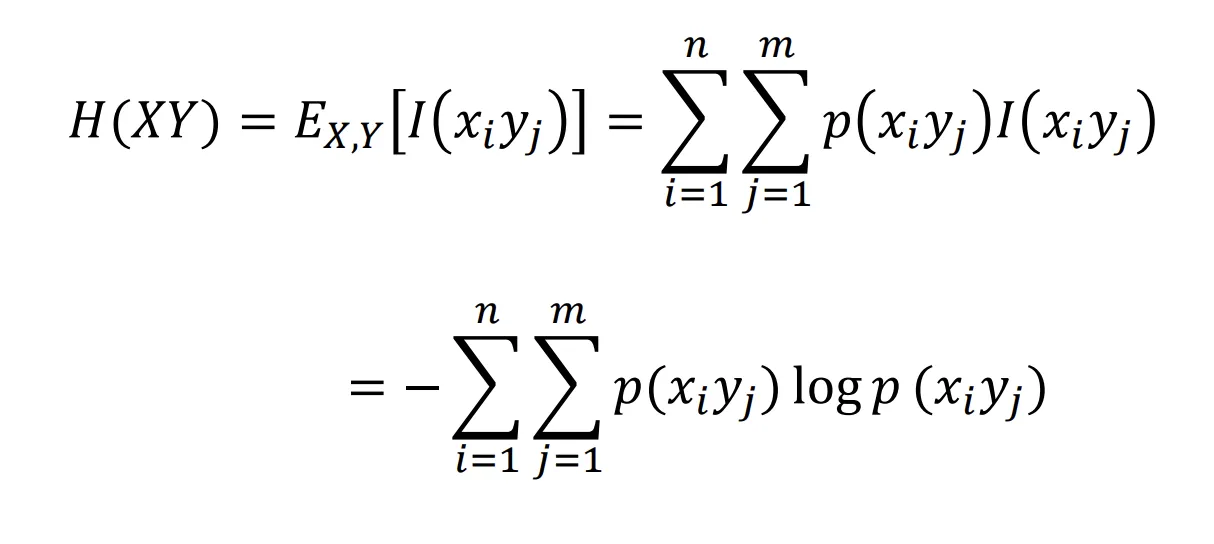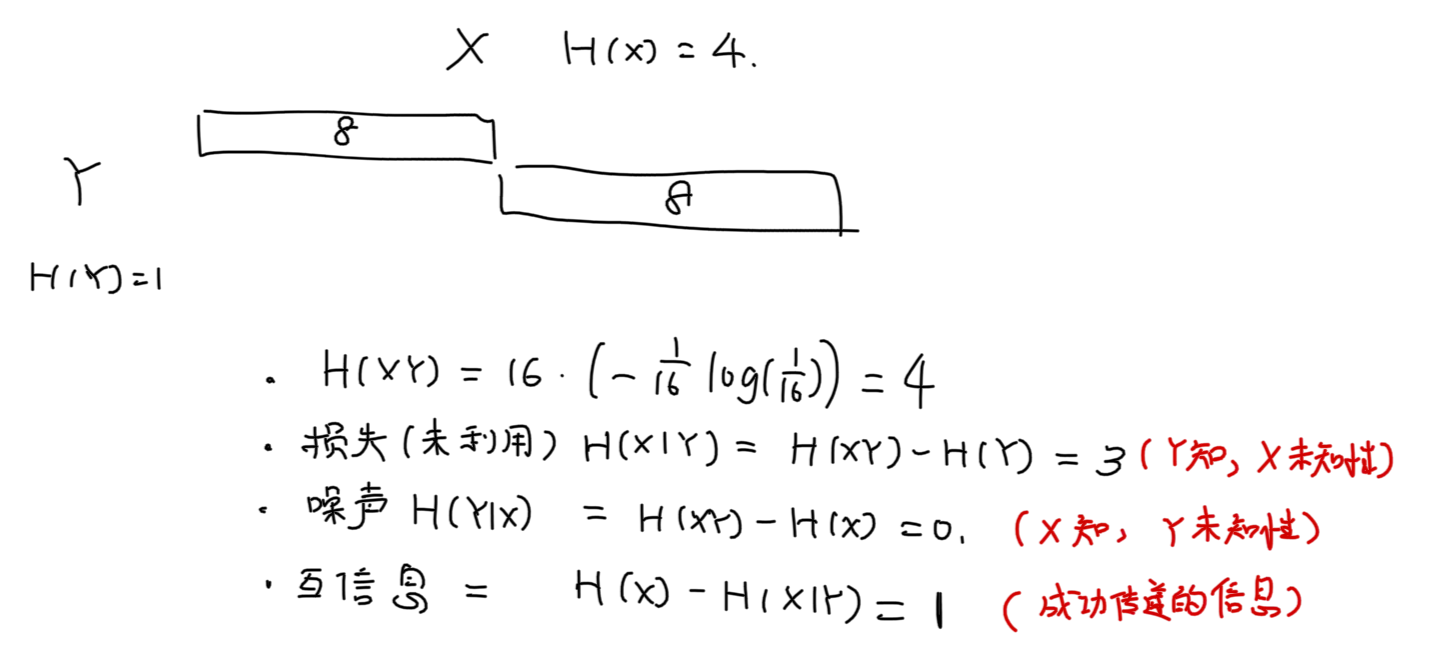CH2-信息的统计

• [自信息]

  • 概率小 50%，信息量 + 1

• [条件自信息]

  • ...

• **[互信息]

  • 用于衡量两个随机变量之间相互依赖性的量（成功传输的信息）

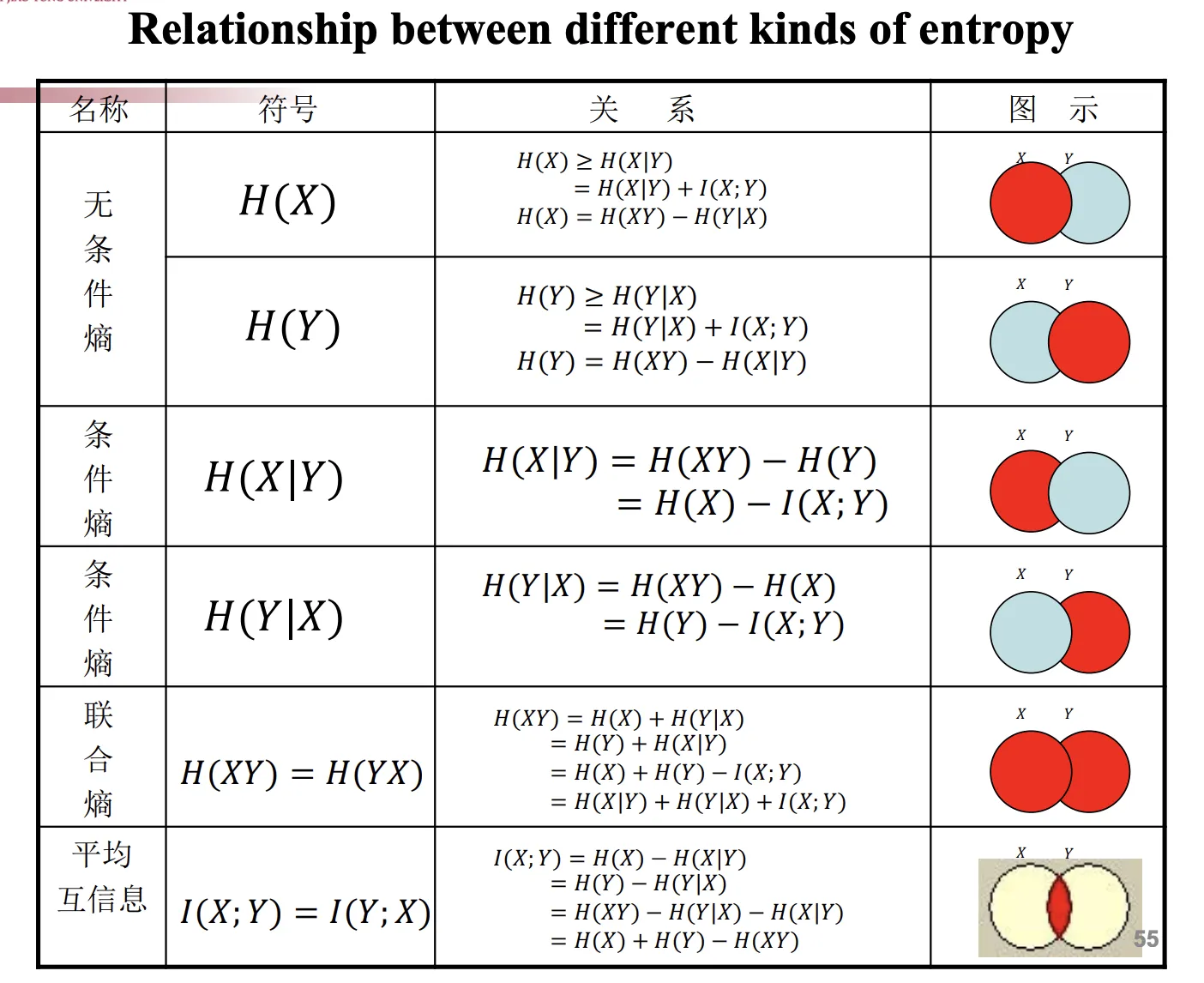
• [信源熵]

  • 就是自信息的期望, 对于无记忆信源. 是一个先验概率:
  • 单位 bit/symbol （信息每符号）。符号几率越平均，熵越大
    • 还有后验概率版本，即接收到了以后反算熵.

• [条件熵]

  • 即条件自信息的期望. 为已知随机变量 的条件下随机变量 的不确定性.

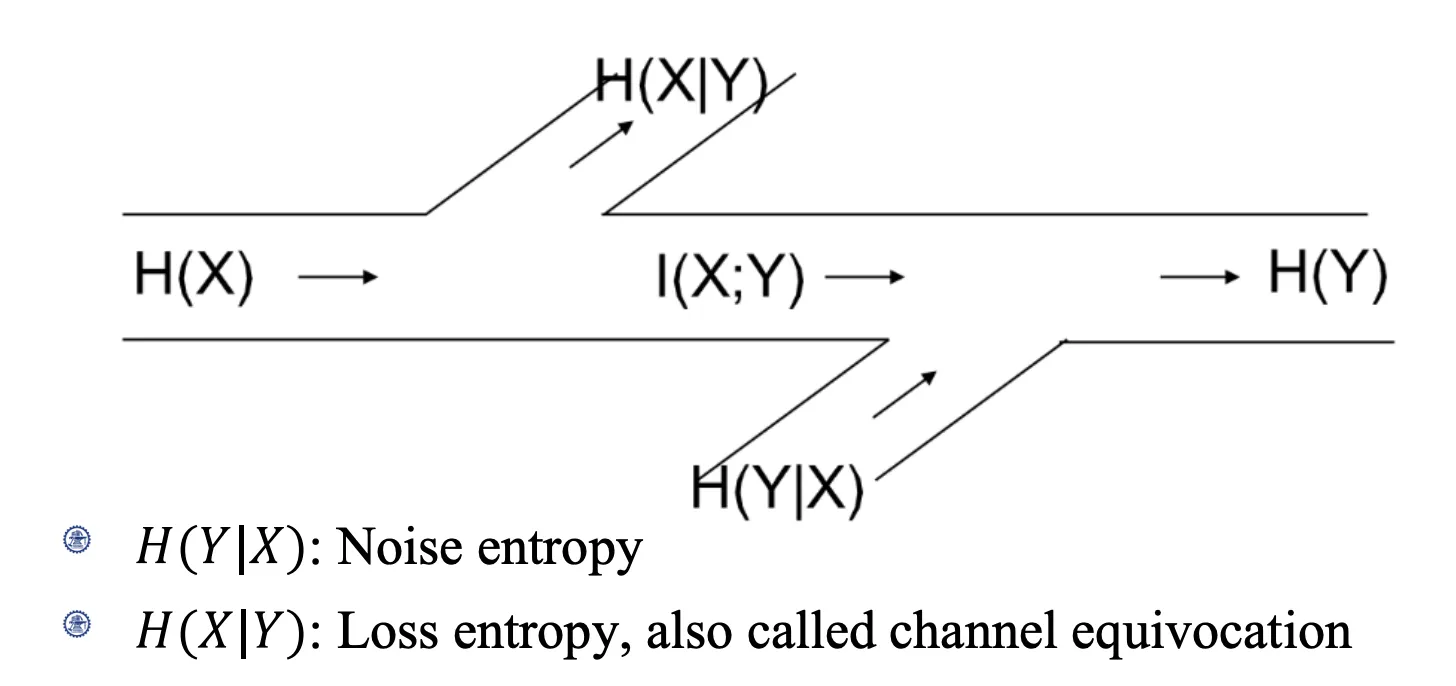
  • [噪声熵]: X 给到 Y 以后 Y 还有多少噪声.

    • 

  • [损失熵]:

    • X 的多少信息没传过去.
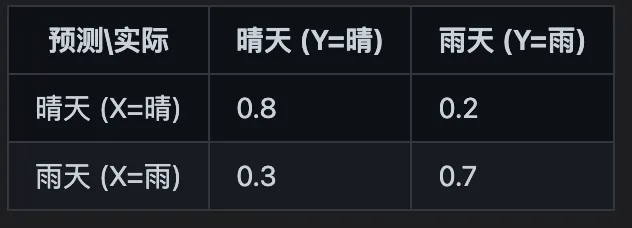
      • 例子： 必导致 , 必导致 ，
        • 则噪声熵为 ，损失熵 ，联合熵
    • 

• [联合熵 Joint Entropy]:

  • 

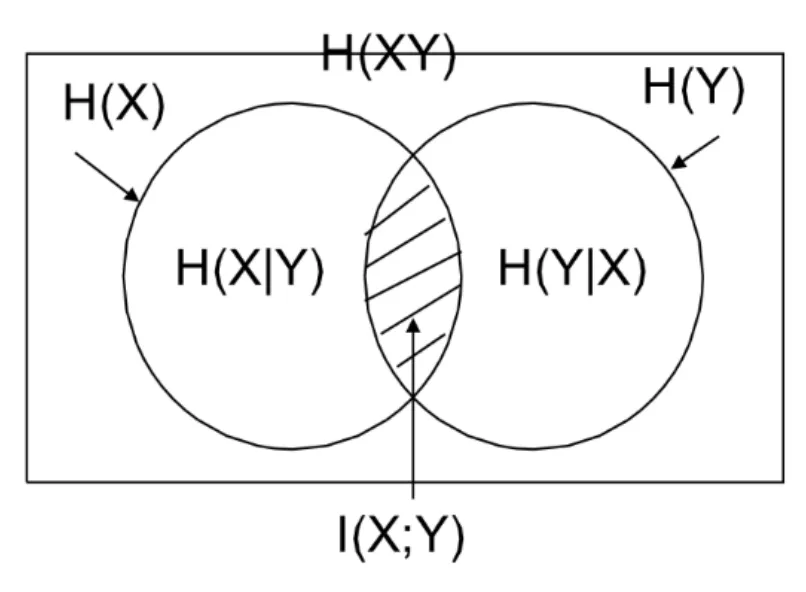
• 不确定性图:

  • 
  • 
  • 
  • 例:
    • 
    • 
  • 例:
    • 

• [熵函数的属性]

  • 非负性
  • 对称性: 交换概率，熵不变
  • 确定性：如果存在一个概率 = 1，则信息量为 0.
  • 扩展性: 将其中一个 分出一个极小量到另一个符号，熵不变.
  • 强可加性:
    • 可加性: s-独立时有
  • 增性:
    • 将其中一个符号 拆分成若干个符号（概率和为 ），熵增加.
  • 上凸性:
    • 对概率向量 ， 是上凸的
  • 极限性质：
    • 对于离散信源, 当各个符号概率一样的时候， 最大.

例题

• [问] 信源的熵
  • 可以用变长码（哈夫曼编码）来表示这些符号，可以做到平均编码长度为