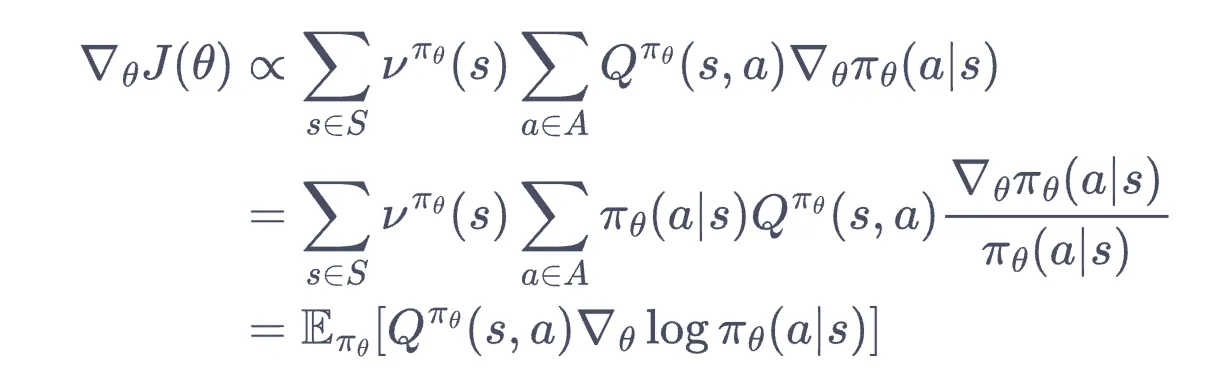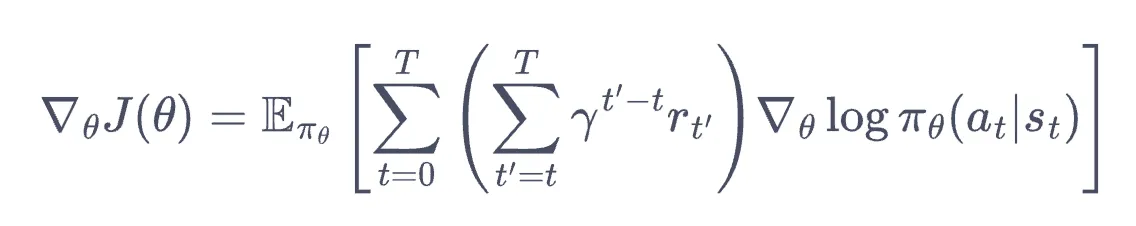其他一样. - how to

之前的算法基于价值，没有显式策略（策略就是选最大动作价值的动作）。下述 REINFORCE 方法基于策略.
设 $pi_theta$ 是策略，处处可微，要学习的参数为 $theta$
目标是最大化 : $$J(theta) = EE_(s_0) [V^(pi_theta) (s_0) ]$$
设状态访问分布为 $nu^pi$（无穷步状态概率加权向量，见第三章），有:
- 提示: $(log f)^prime = f^prime / f$
另一证明:
- https://paddlepedia.readthedocs.io/en/latest/tutorials/reinforcement_learning/policy_gradient.html
- 此图第一行少写了一个 $sum$
- 这里 $T(s, a)$ 是执行 $a$ 后转移到 $s$ 的概率.

蒙特卡洛 REINFORCE

考虑用蒙特卡洛方法估计，对有限步的环境来说，依据上式有:
- 其中 $T$ 为最大步数. 小括号内就是 $G_t$，下面第二张图中以 $psi_t$ 表示.
训练步骤
网络结构:
- Input: 可微状态
- Output: 离散动作的概率多项分布
- 损失函数: 上述梯度更新公式（去掉微分符号）

1
class PolicyNet(torch.nn.Module):
2
    def __init__(self, state_dim, hidden_dim, action_dim):
3
        super(PolicyNet, self).__init__()
4
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
5
        self.fc2 = torch.nn.Linear(hidden_dim, action_dim)
6

7
    def forward(self, x):
8
        x = F.relu(self.fc1(x))
9
        return F.softmax(self.fc2(x), dim=1)
10

11
class REINFORCE:
12
    def __init__(self, state_dim, hidden_dim, action_dim, learning_rate, gamma,
13
                 device):
14
        self.policy_net = PolicyNet(state_dim, hidden_dim,
15
                                    action_dim).to(device)
28 collapsed lines
16
        ...
17

18
    def take_action(self, state):  # 根据动作概率分布随机采样
19
        state = torch.tensor([state], dtype=torch.float).to(self.device)
20
        probs = self.policy_net(state)
21
        action_dist = torch.distributions.Categorical(probs)
22
        action = action_dist.sample() # 随机选一个
23
        return action.item()
24

25
    def update(self, transition_dict):
26
        reward_list = transition_dict['rewards']
27
        state_list = transition_dict['states']
28
        action_list = transition_dict['actions']
29

30
        G = 0
31
        self.optimizer.zero_grad()
32
        for i in reversed(range(len(reward_list))):  # 从最后一步算起
33
            reward = reward_list[i]
34
            state = torch.tensor([state_list[i]],
35
                                 dtype=torch.float).to(self.device)
36
            action = torch.tensor([action_list[i]]).view(-1, 1).to(self.device)
37
            log_prob = torch.log(self.policy_net(state).gather(1, action))
38
            G = self.gamma * G + reward
39
            loss = -log_prob * G  # 每一步的损失函数
40
            loss.backward()  # 反向传播计算梯度
41
        self.optimizer.step()  # 梯度下降
42

43
# 其他一样.

考虑最优情况的正确性：若 $G_1 = 200, G_2 = -200$，则会学到使得 $p_1$ 尽可能大（取 -log 后尽可能小，损失尽可能小），$p_2$ 尽可能小（取 -log 后极大，损失极小）
- softmax 应该能防止数值爆炸.

优化问题，神经网络和强化学习

…