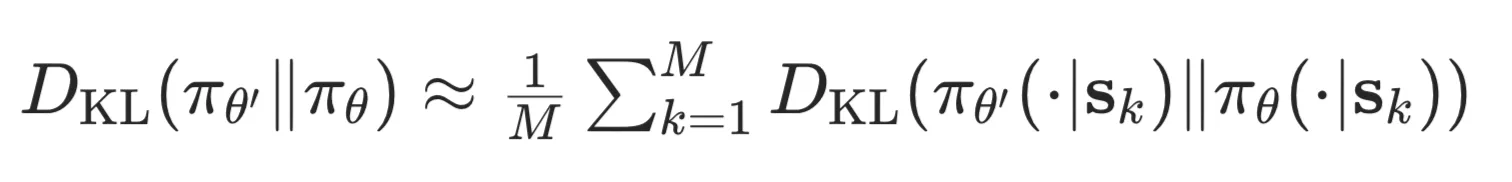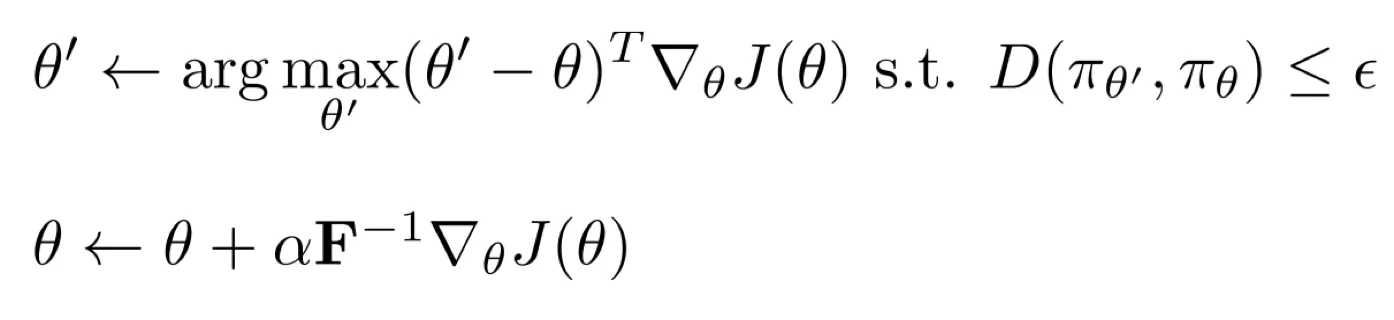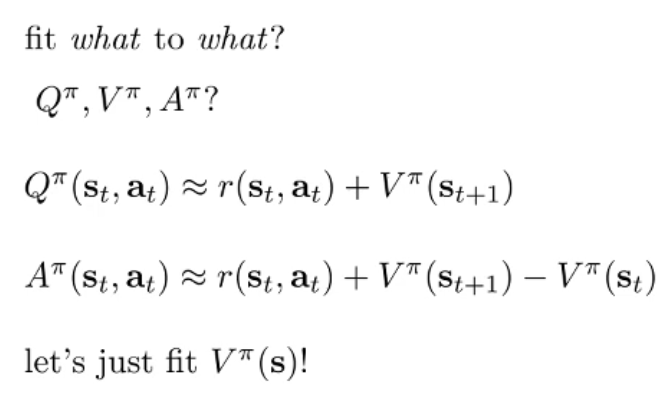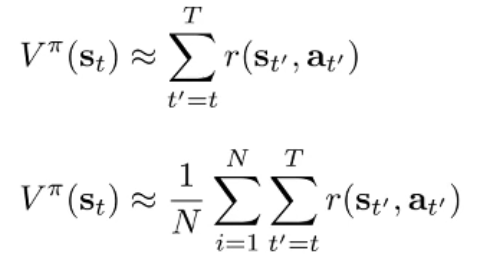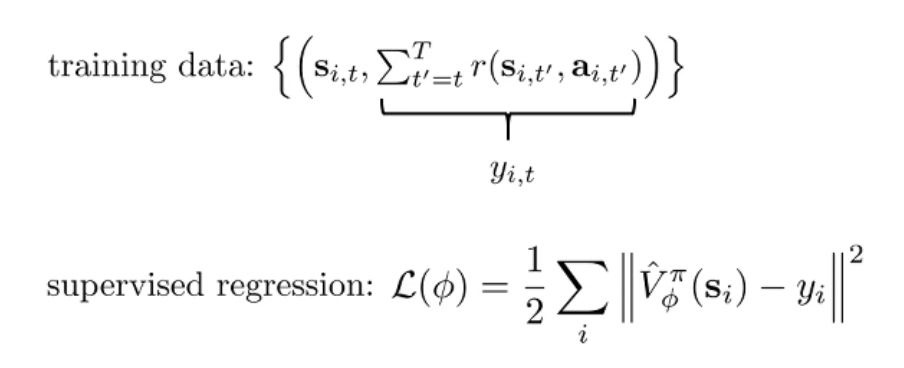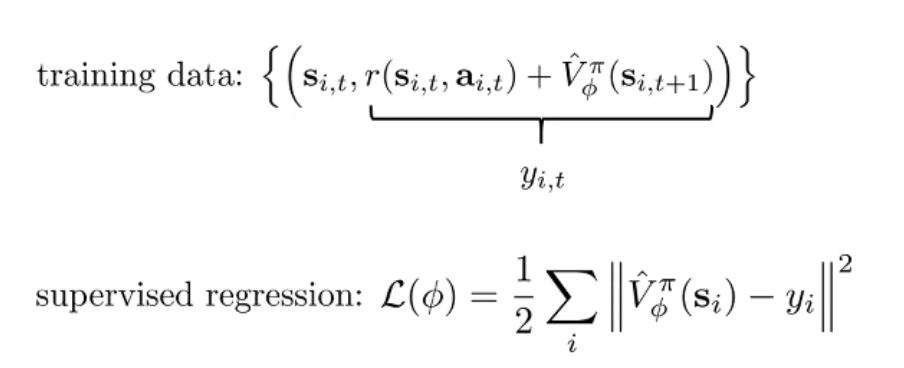https://rail.eecs.berkeley.edu/deeprlcourse-fa23/
- hw1: https://rail.eecs.berkeley.edu/deeprlcourse-fa23/deeprlcourse-fa23/static/homeworks/hw1.pdf
- hw2:
- 讲师:Sergey Levine https://people.eecs.berkeley.edu/~svlevine/ (some talks here)
符号
-
: 策略的累积奖励的期望,需要最大化
-
顺序:
-
: 轨迹,表示所有
-
:状态 下采取 的概率
-
状态价值函数 state-value function,即还不确定
-
动作价值函数 action-value function,即确定了
- 有
FAQ
何时来的?

- 从右往左看. 导数怎么传递到 上的?
强化学习类型
- Policy Gradient: 求 对 的导数.
- 训练:
- Actor: 输入
[机械臂状态,观测] - 输出
[动作]或者[动作的概率分布]
- Actor: 输入
- 推理: 一样
- 训练:
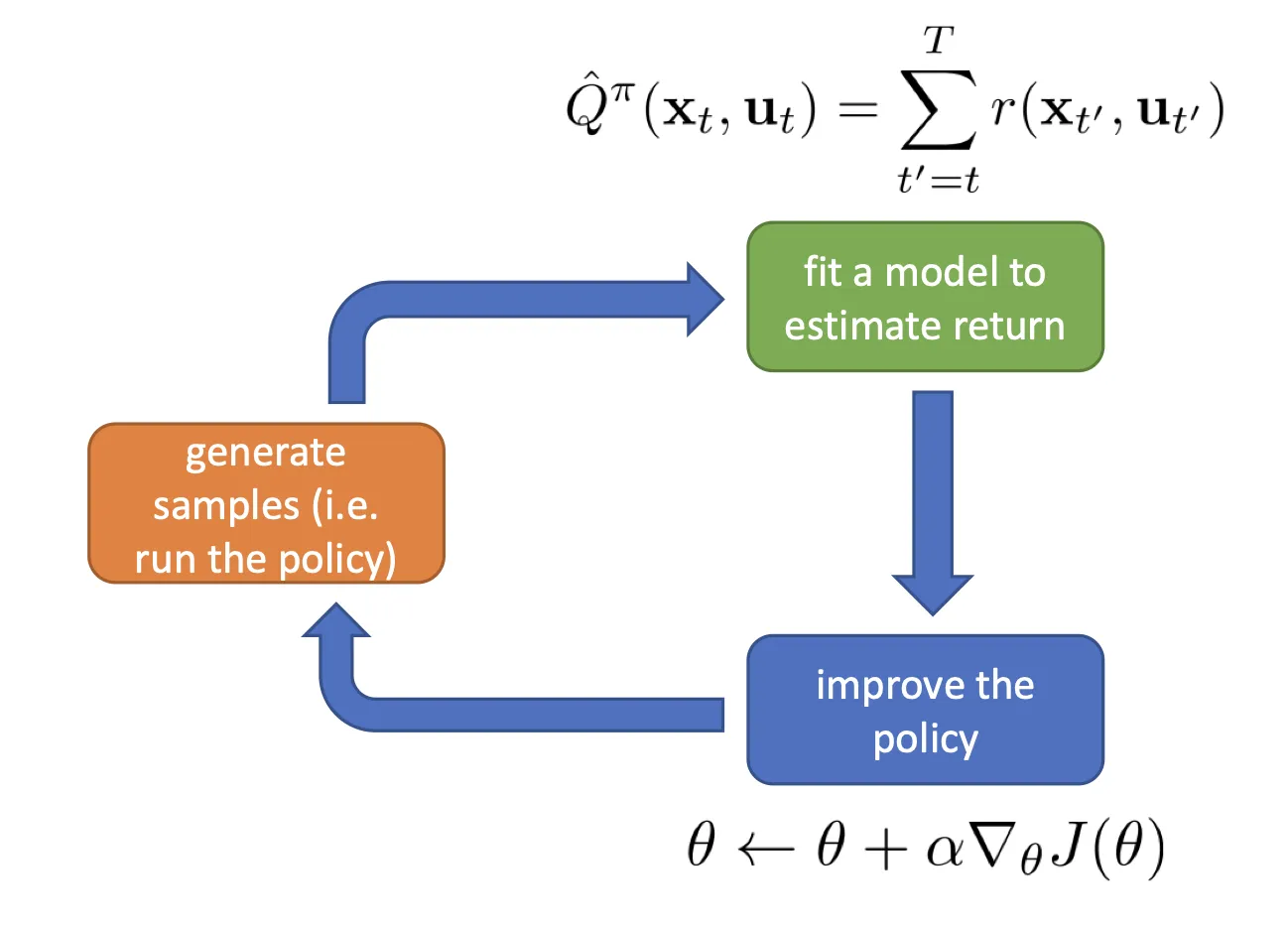
- Value Based (DQN): 直接训练一个 Q / V,取最大值对应的动作索引 (no explicit policy)
- Actor-Critic: 有 A 有 Q
- Model-based: 有模型自行估计 经过 如何转移 ( learn )
On-off policy
-
off-policy: able to improve the policy without generating new samples from that policy
-
on-policy: any time the policy is changed (even a little bit) we need to generate new samples.
-
(and there is offline-RL)
Lec5 Policy Gradients
- https://rail.eecs.berkeley.edu/deeprlcourse-fa23/deeprlcourse-fa23/static/slides/lec-5.pdf
- Maximum likehood 仅仅让 朝着“这批动作出现概率最大”的方向演进.


- [later, qm] 这不是模仿学习么,哪儿来的代码
1logits = policy(states)2loss_fn = torch.nn.CrossEntropyLoss()3loss = loss_fn(logits, actions) # 离散动作4loss.backward()5gradients = [p.grad for p in policy.parameters()]- 问题:奖励方差大,训练效率低下。好轨迹梯度可能为 0(累积奖励 0),有效奖励信号丢失.
例子:高斯 policy
这里距离是马氏距离,用协方差使得距离评估更准.
两种优化
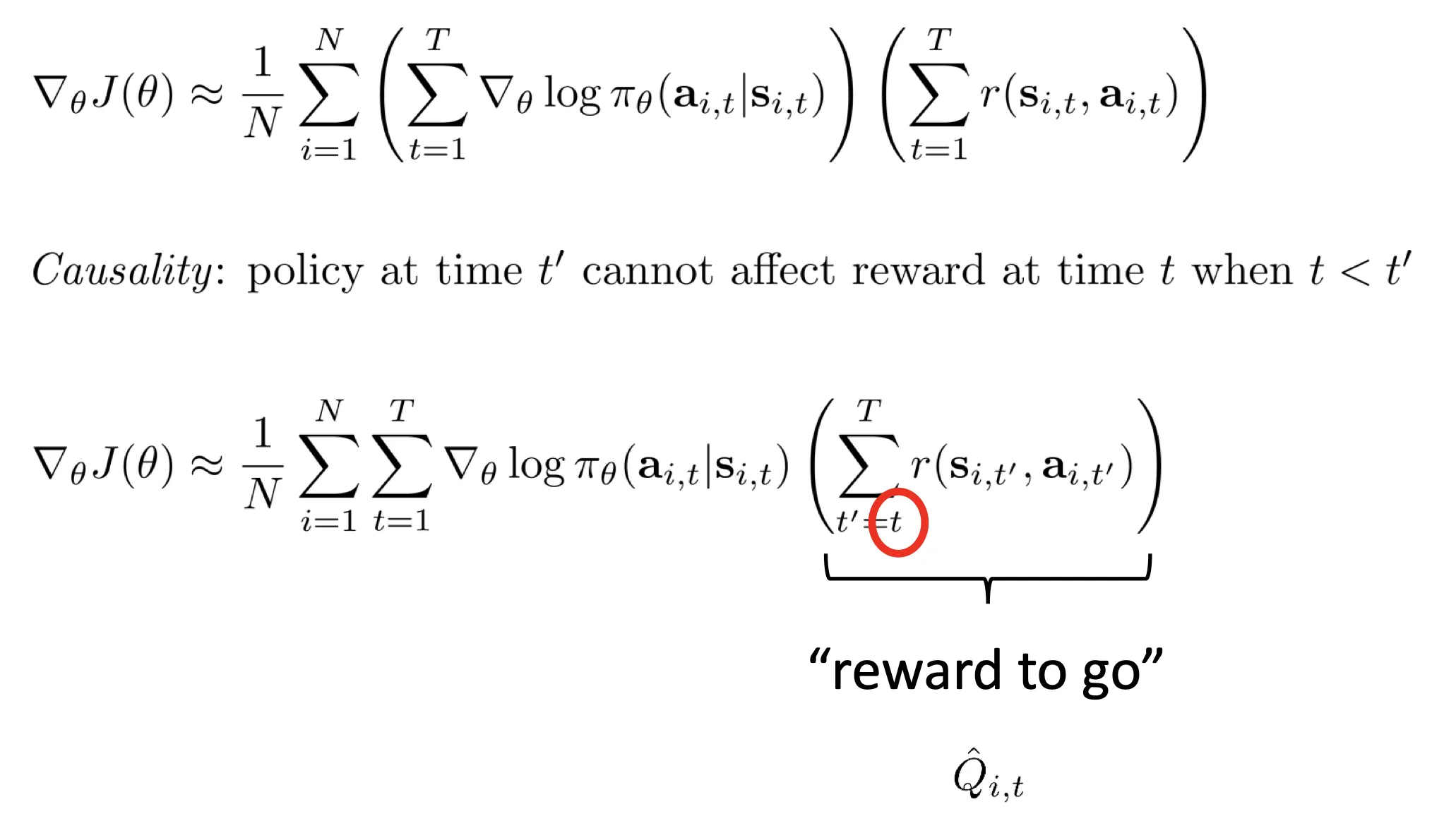
- 换种形式: reward to go:
- 等等先换一个话题,我们求一个 baseline 并改写奖励为
 ,目的是使梯度方差最小。推导出最优的 为:
,目的是使梯度方差最小。推导出最优的 为:

- 其中:

- 结合以上两个优化,得到:

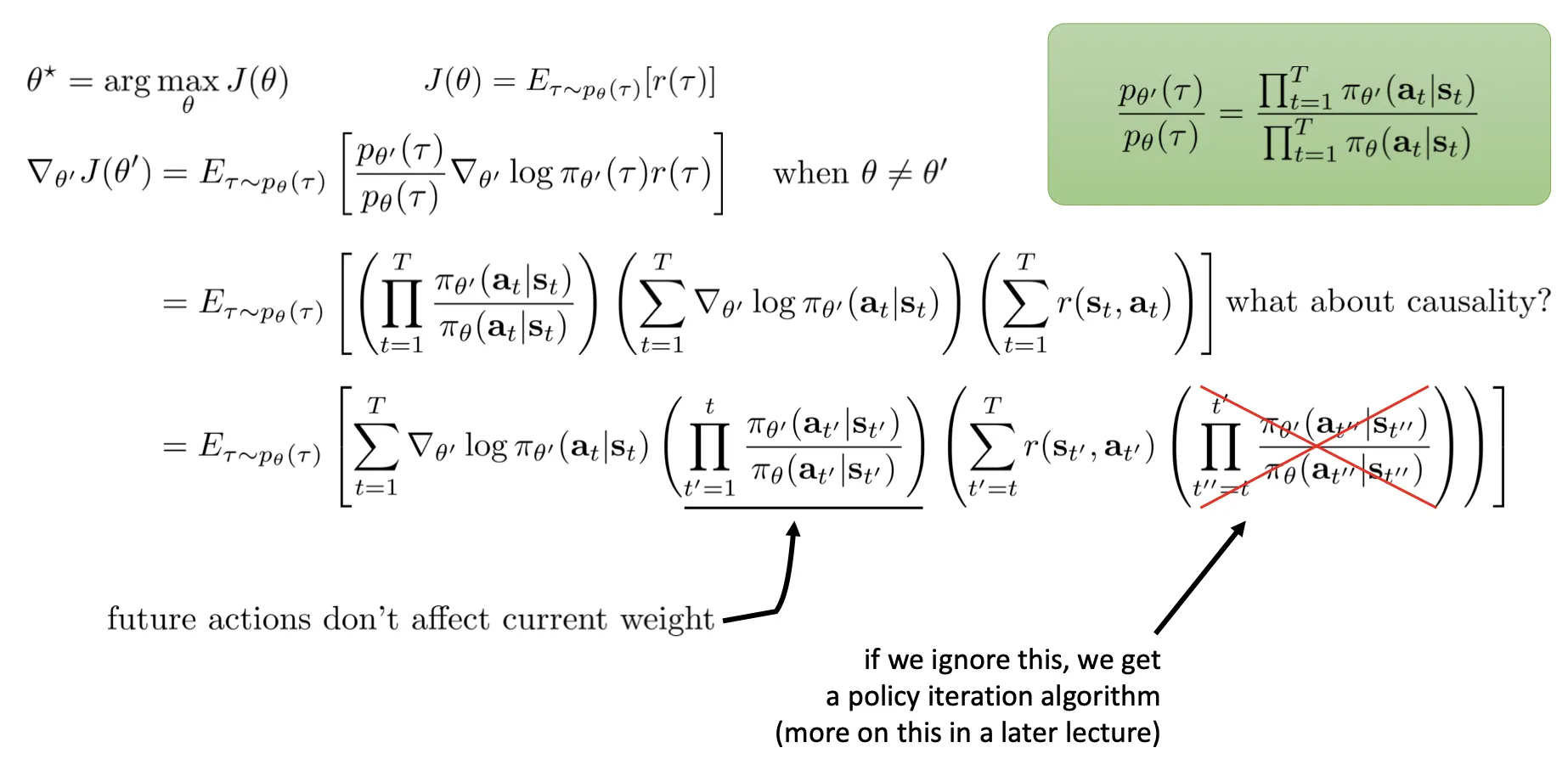
为什么 PG 必须是 on-policy
上述公式是对 求导, 必须是最新的,求的梯度才有意义。导致训练效率很低. 当然你可以多采样几次,相当于 batch 大很多.
importance sampling
- 这个公式就是 IS:


- [ok]
- [grep] 注意上图 那个概率在下图这里已经改写为乘积完毕的形式 .

- 最后还是改用自动求导了,因为显示计算 那一项开销太大. 而 那一项正好对应平方误差.
优化的梯度下降?
- 能直接走到最好的 吗?

- 上图第一个方法“参数距离约束”依赖于参数的具体形式,不好。
- 上图 KL 散度:
 通过采样计算.
通过采样计算. 
1# states: (B, S_dim) -> logits: (B, A_dim)2logits_old = policy_old(states)3logits_new = policy_new(states)4
5# 将 logits 转换为概率分布. 连续动作用 Normal 代替 Categorical6dist_old = torch.distributions.Categorical(logits=logits_old)7dist_new = torch.distributions.Categorical(logits=logits_new)8
9# 对所有样本取平均,得到最终的 KL 散度值10kl_divergence = torch.distributions.kl.kl_divergence(dist_new, dist_old).mean()- 进一步:通过 Fisher 信息矩阵近似展开 KL 散度:

- 可以通过采样来估计 .

- WHY this formula? see: [ai]

- 上图两种训练方法。选择 : natural gradient. 选择 : trust region policy optimization
- Lec5 end!
Hw1
1.1 Given
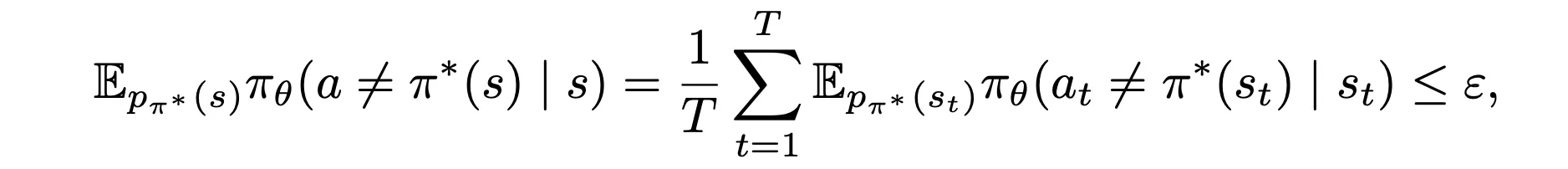 show:
show: 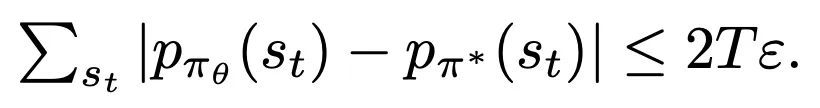
- see: https://blog.csdn.net/weixin_55471672/article/details/138329230
- 第一题我证半天不会证,给我整笑了.
1.2

- holy!
- The Off-policy policy gradient: 这张图简单易懂:

2 Editing Code
如何可视化: tensorboard --logdir=/home/julyfun/Documents/GitHub/homework_fall2023/hw1/data/q1_bc_ant_HalfCheetah-v4_2 3-11-2025_00-00-06/
“
- Ant-v4:
1Eval_AverageReturn : 4795.38281252Train_AverageReturn : 4681.8916739358163Training Loss : 0.0011749982368201017- Walker-2d 只有 2d 物理
1Eval_AverageReturn : 998.9587402343752Train_AverageReturn : 5383.3103251776683Training Loss : 0.01655399613082409走的不太行,能往前冲一点
- HalfCheetah
1Eval_AverageReturn : 4070.51464843752Train_AverageReturn : 4034.79998349650673Training Loss : 0.004244370386004448
- Hopper
1Eval_AverageReturn : 1542.3718261718752Train_AverageReturn : 3717.51299361823073Training Loss : 0.010719751007854939看视频跳的还可以
 关于这个 Hopper 任务, batchsize: (我本来还想搞 N 条轨迹来实验,但是这个专家数据只有若干个 s-a pair,没法搞)
关于这个 Hopper 任务, batchsize: (我本来还想搞 N 条轨迹来实验,但是这个专家数据只有若干个 s-a pair,没法搞)
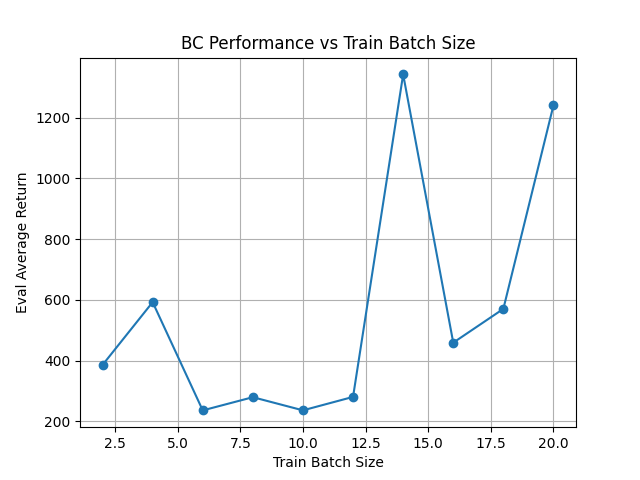

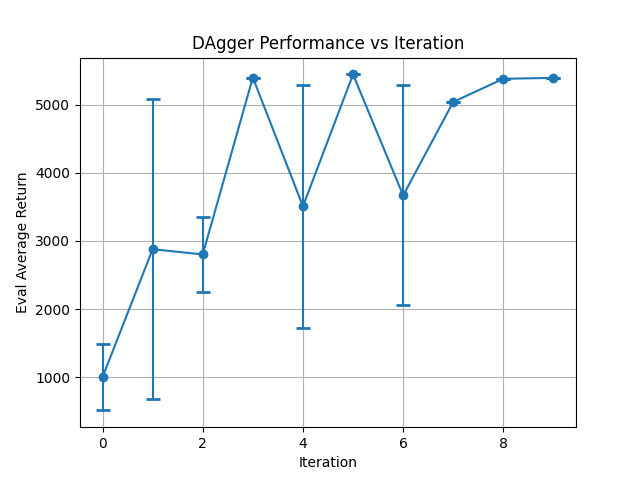
3. Dagger
- Walker-2d
- 这里
batch_size default=1000参数不用调,因为 train 的时候只拿出前train_batch_size=100个. 是公平的.
1Eval_AverageReturn : 998.9587402343752Eval_StdReturn : 488.84045410156253Train_AverageReturn : 5383.3103251776684Train_StdReturn : 54.152515638717895Training Loss : 0.016553996130824096
7********** Iteration 1 ************8Eval_AverageReturn : 5408.24316406259Eval_AverageEpLen : 1000.010Train_AverageReturn : 1130.50415039062511Train_StdReturn : 583.066223144531212Training Loss : 0.02255682088434696213
14********** Iteration 2 ************15Eval_AverageReturn : 5389.767089843754 collapsed lines
16Eval_StdReturn : 0.017Train_AverageReturn : 5411.1459960937518Train_StdReturn : 0.019Training Loss : 0.012993226759135723-
实验时在默认命令上尽量少改动.
-
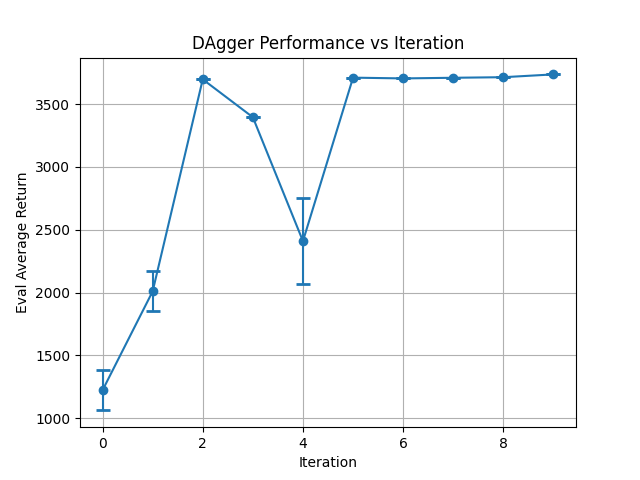
Walker2d DAGGER:

-
强制不收集新数据:
if itr == 0:=>if itr == 0 or True:(后来我改了其他代码,可以 no_dagger 多轮执行)
-
no-dagger Step 0: 会 terminate

-
DAgger Step 9:

-
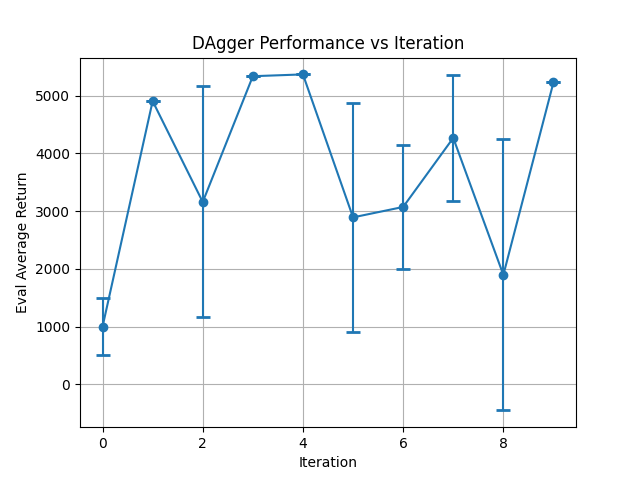
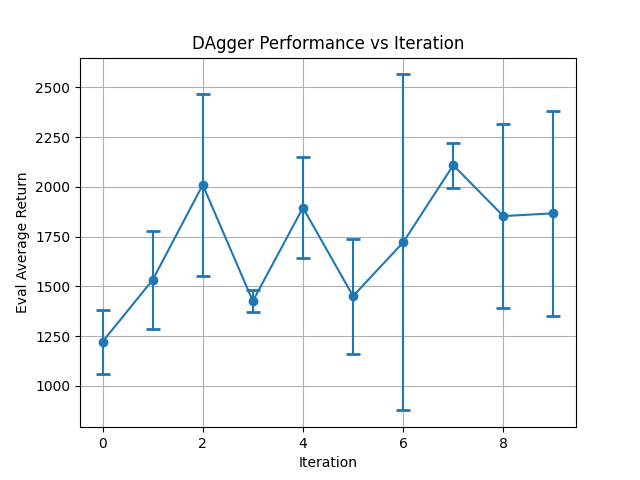
Hopper DAgger:

-
Hopper no dagger

-
DAgger Step 9:

Lec6 Actor Critic
- https://www.youtube.com/watch?v=wr00ef_TY6Q&list=PL_iWQOsE6TfVYGEGiAOMaOzzv41Jfm_Ps&index=21
- https://rail.eecs.berkeley.edu/deeprlcourse-fa23/deeprlcourse-fa23/static/slides/lec-6.pdf
- 为什么加入 baseline 项可以减少方差呢?
- 因为 Q(s, a) - V(s) 可以分离出动作 本身的价值,降低梯度波动.
- 我的理解是对于完美的 Q 来说减了 V 也不会降低方差了.

- 我们发现 A(优势函数)只需要 fit V.

- 如何定义 呢? 下面这个公式更好,但是这需要从同一个 出发多次采样,除了仿真以外是不可能的!
- 所以我们采用上面那个公式.

- 第一版训练方法出炉!

- Can we do better? 直接用 V 估计之后的收益,尽管一开始不准.
- Lower variance, Higher bias! (“because it’s using b hat instead of a single sample estimator”, 或者说 是一个期望而不是一个采样. )

- [bookmark] https://www.youtube.com/watch?v=KVHtuwVhULA&list=PL_iWQOsE6TfVYGEGiAOMaOzzv41Jfm_Ps&index=23&t=12s
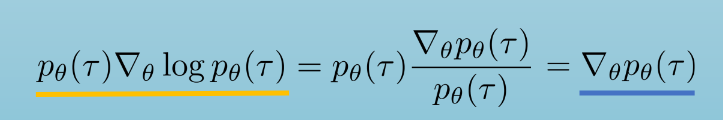
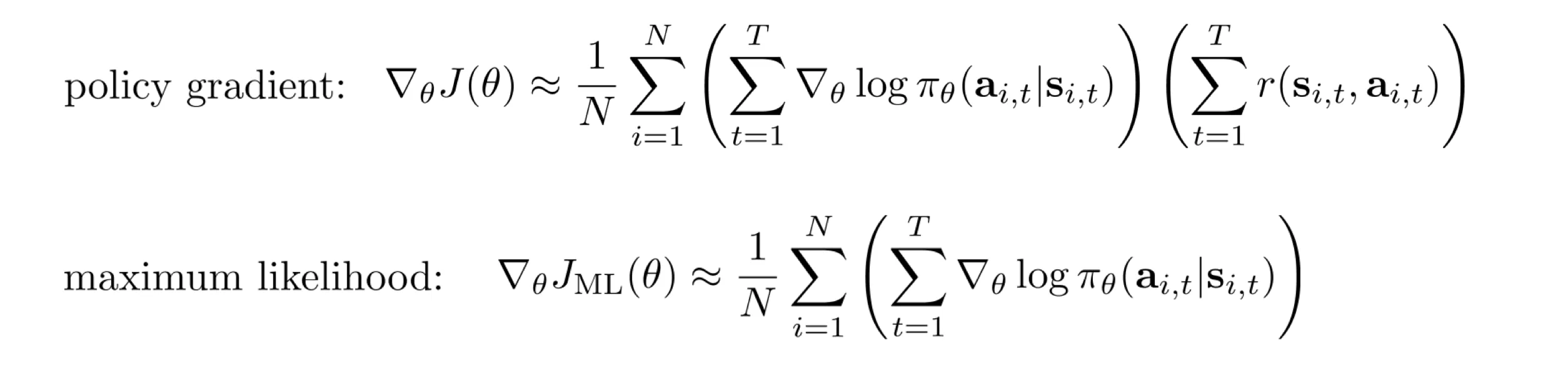
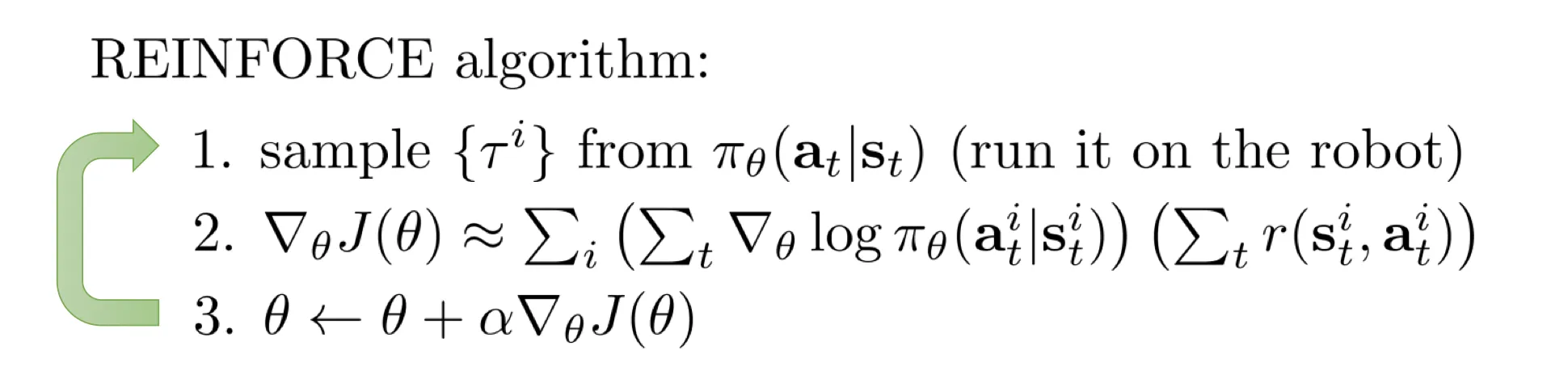
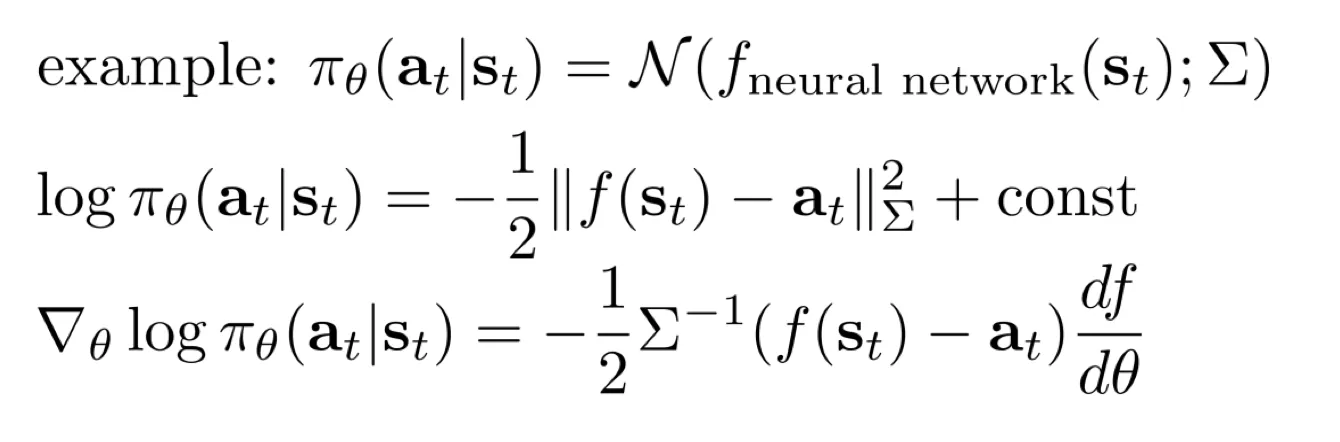
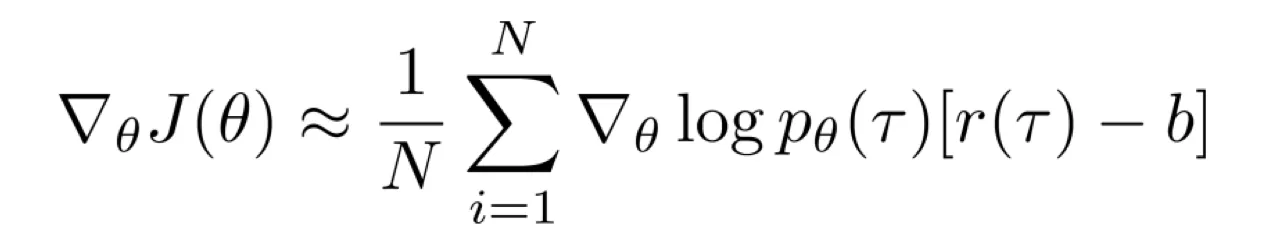 ,目的是使梯度方差最小。推导出最优的 为:
,目的是使梯度方差最小。推导出最优的 为:
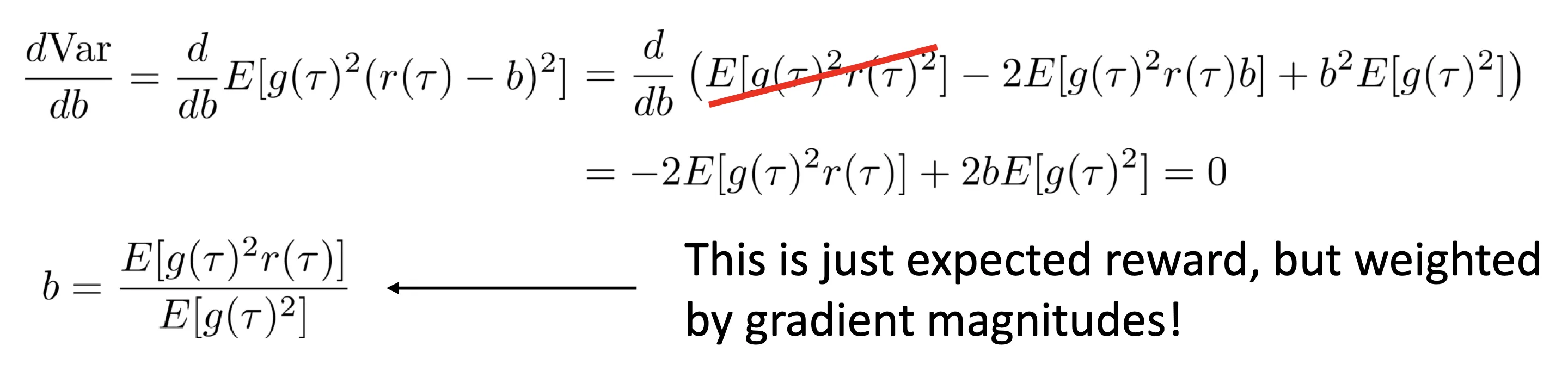
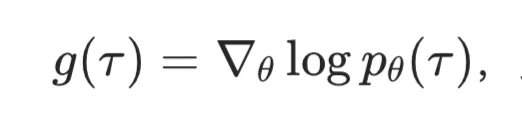
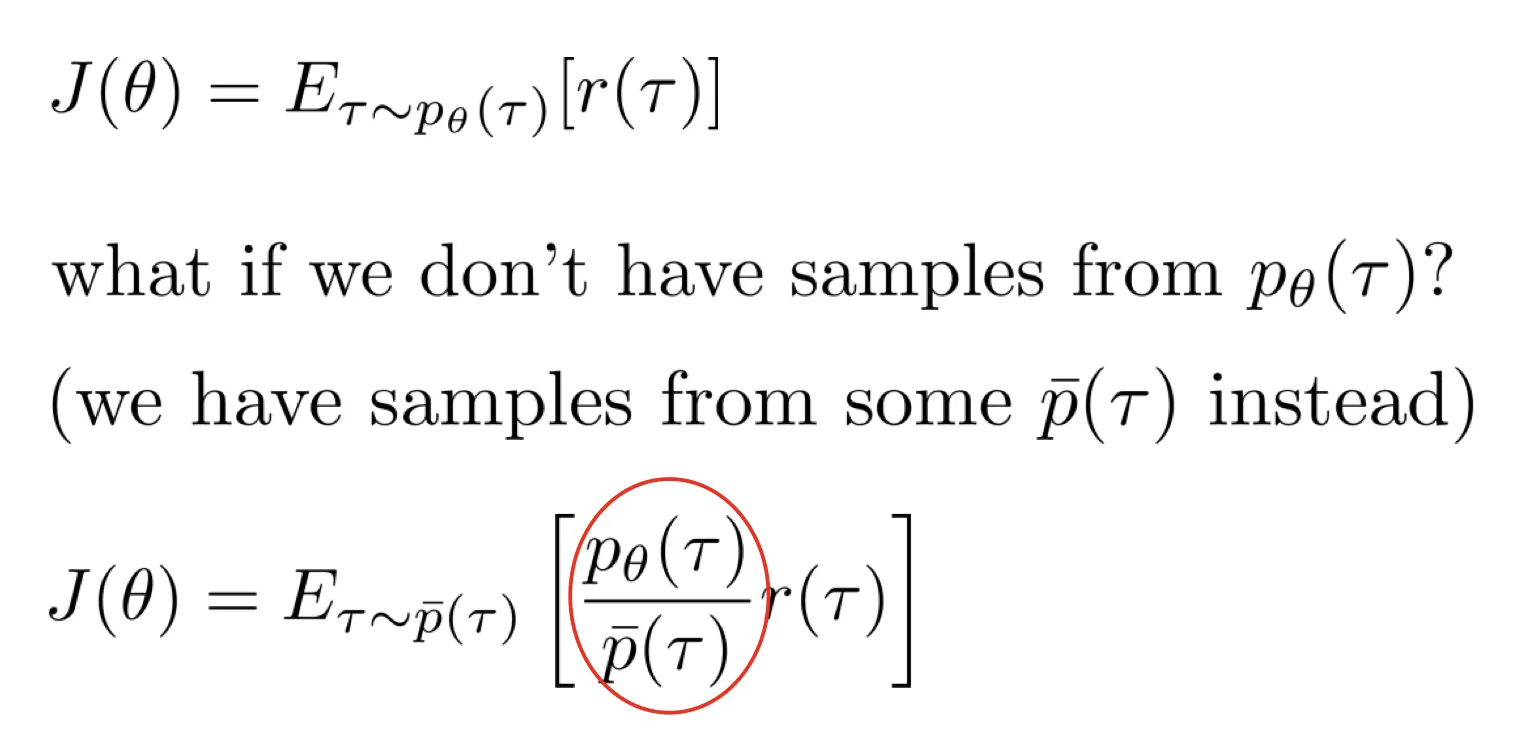


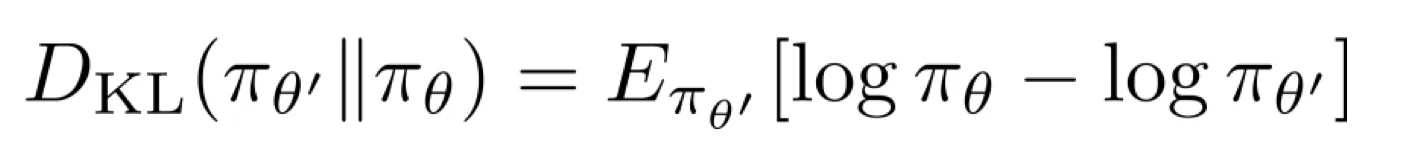 通过采样计算.
通过采样计算.