2 多臂老虎机
符号
- $cal(A)$: 动作集合 $cal(R)$: 奖励概率分布，动作 $a$ 对应一个奖励分布 $cal(R)(r | a)$
- 对动作 $a$，定义其期望奖励为 $Q(a)$
- 最优期望奖励 $Q^* = max_(a in cal(A)) Q(a)$
- 懊悔 $R(a) = Q^* - Q(a)$
- $limits(Q)^("hat")$: 对 $a$ 的期望奖励估值
名称
- MAB: 多臂老虎机
- UCB: 上置信界法
问题表述
多臂老虎机是无状态的强化学习，即与环境交互不会改变环境。在下述算法里，每个老虎机的奖励服从伯努利分布，即以 $p_i$ 的概率获得 $1$
$epsilon$ 贪心算法
$$ a_t = cases( arg max_(a in cal(A)) Q^"hat" (a) & "采样概率" 1 - epsilon, "从" cal(A) "随机选择" & "采样概率" epsilon ) $$
以 $epsilon$ 的概率随机探索一个。结果由于随机的部分，懊悔是线性增长的。
随时间衰减的 $epsilon$ 贪心算法
$epsilon_t = 1 / t$
测试时 $K = 10$（老虎机个数），结果累计懊悔是 $ln$ 形式增长的。
上置信界算法
用到了霍夫丁不等式。每一时刻设一个概率 $p = 1 / t$。对于每个动作 $a$ 算出一个 $U_t^"hat" (a)$ s.t. $p = e^(-2N_t(a)U_t(a)^2) (<=> U^"hat"_t (a) = sqrt((-log p) / (2 N_t (a))) )$，根据霍夫丁不等式必有: $Q_t (a) < Q^"hat"_t (a) + u$ 至少以 $1 - p$ 概率成立，称不等式右边为期望奖励上界（其实是大概率上界）。当 $t$ 增大时该可能性极大。
实操时, $U^"hat"t (a) = sqrt((-log p) / (2 (N_t (a) + 1)))$，每次选择 $a = arg max(a in cal(A)) Q^"hat" (a) + c dot U^"hat" (a)$ 其中 $c$ 为控制不确定性比重的系数。ipynb 中 $c = 1$
累计懊悔也是 $ln$ 形式:
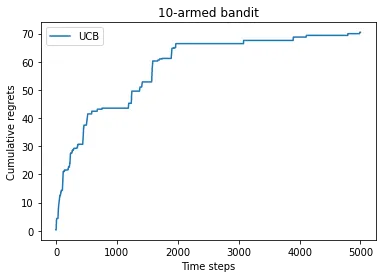
汤普森采样算法
若拉杆 $m_1$ 次奖励为 $1$，$m_2$ 次奖励为 $0$ ，则大胆假设拉杆的奖励概率（注意奖励概率为 $p$，每次要么得 $1$ 要么得 $0$）的概率分布为 $Beta(m_1 + 1, m_2 + 1)$
那么每步怎么做决策呢？我们已经大胆假设了所有拉杆的奖励的期望的分布，那么就直接对所有拉杆进行一次 $Beta$ 分布上的采样。拉动采样最大的那个