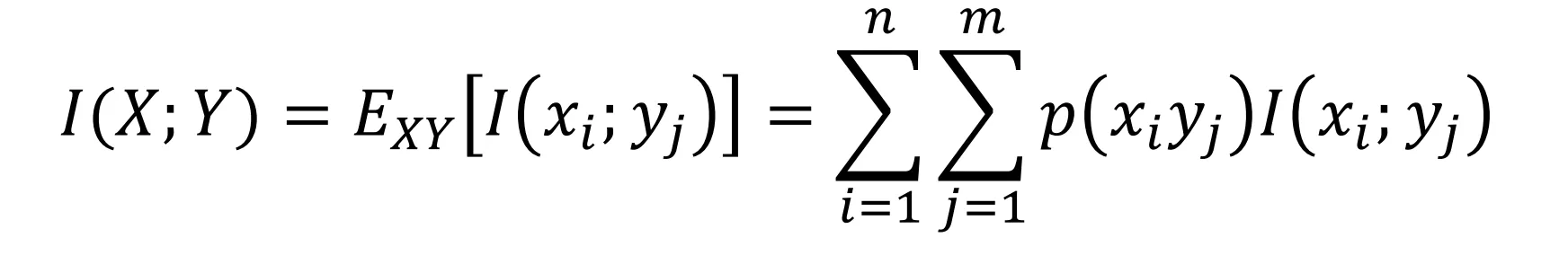- 平均互信息

- 其中 即 X 的信息量减去知道 Y 后 X 的信息量
- (收到 Y) 对于 X 的信息量的贡献.
- 对称性:
- 非负性
- 单次通信可能使 Y 的不确定性增大,但是统计平均一定是不确定性减小
- 凸性
- I(X; Y) 是 关于 向量的一个上凸函数,也就是说 x 知道 的情况下, 比较均匀的分布比较好.
- 信道容量
- 若知道 x, y 的转移矩阵,定义 为信道传输速率,取最优的 分布使得其最大,就得到信道容量 C.
离散单符号信道及其容量
容量
容量就是给定转移矩阵的情况下求 和 的分布使得 最大.
无干扰离散信道
- 输入输出一一对应:
- 多输入对应一输出: 有损失,无噪声, C = max(H(Y))
- 否则无损失,有噪声.
对称性
-
作业里转移矩阵的每一行表示 到各个 分布. 乘法为 . 每一行和为 1.
-
每一行包含的元素相同,则显然噪声熵 与 分布无关. (准对称)
- 最大化 即可最大化
- 所以需要 等概率分布.
- 如果是对称信道,可推出 等概率分布.
-
[转移矩阵]
- 这里一般用第 i 行表示输入信号,第 j 列表示输出信号.
- 每一行和为 1
-
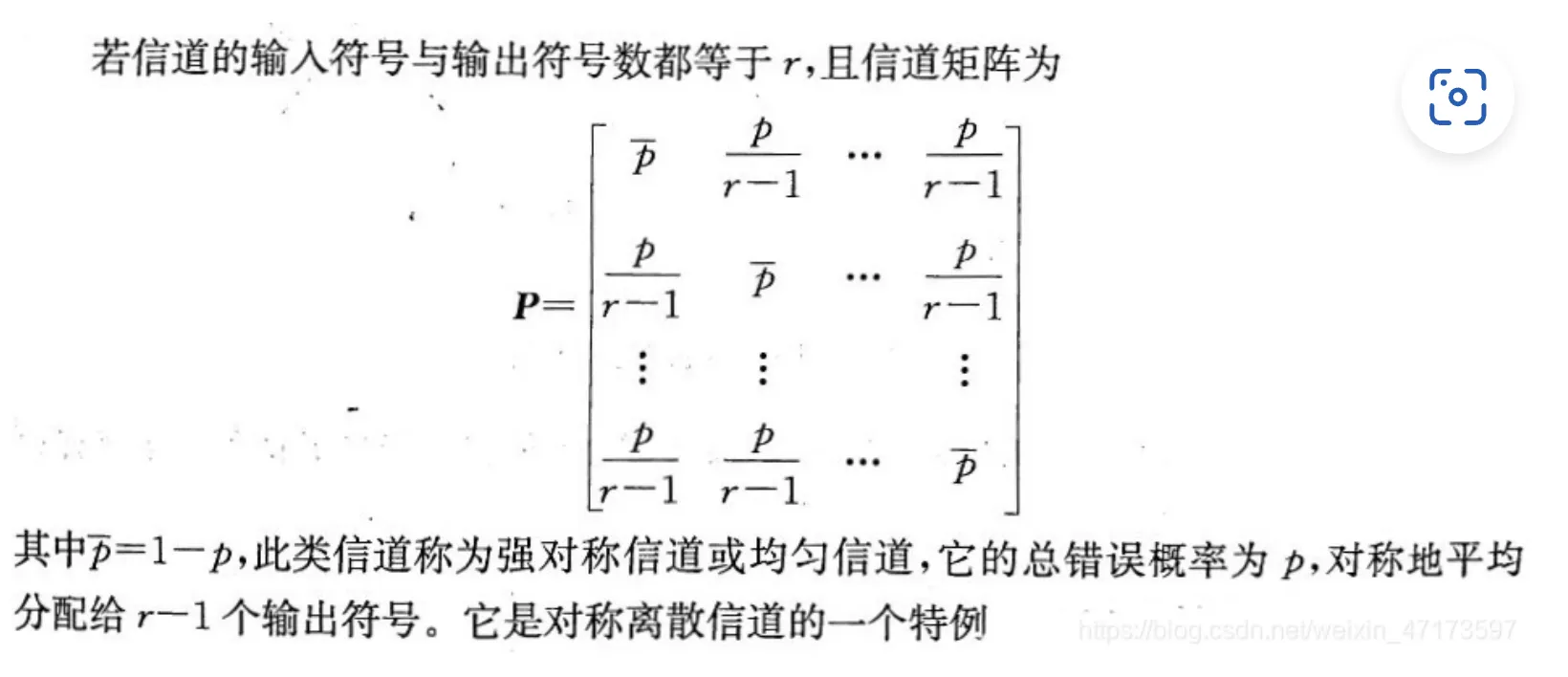
[强对称]
- 均匀分配错误信号.

-
[对称]
- 每一行和每一列包含相同元素.
- 性质:
- 若输入等概率,则输出等概率.
- 容量: 取输入对称,结果为 =
-
[准对称]
- 输入对称而输出不对称,每一行元素相同
- 容量: 需要划分为若干对称矩阵.

-
ref: https://blog.csdn.net/qq_36488756/article/details/110517599
扩展信道
- ex: 知道单个符号的转移矩阵 ,可求两个符号的联合转移矩阵
附录
- 教程: https://www.wbyblog.cn/archives/57.html
- [抄的结论]
- [记忆]