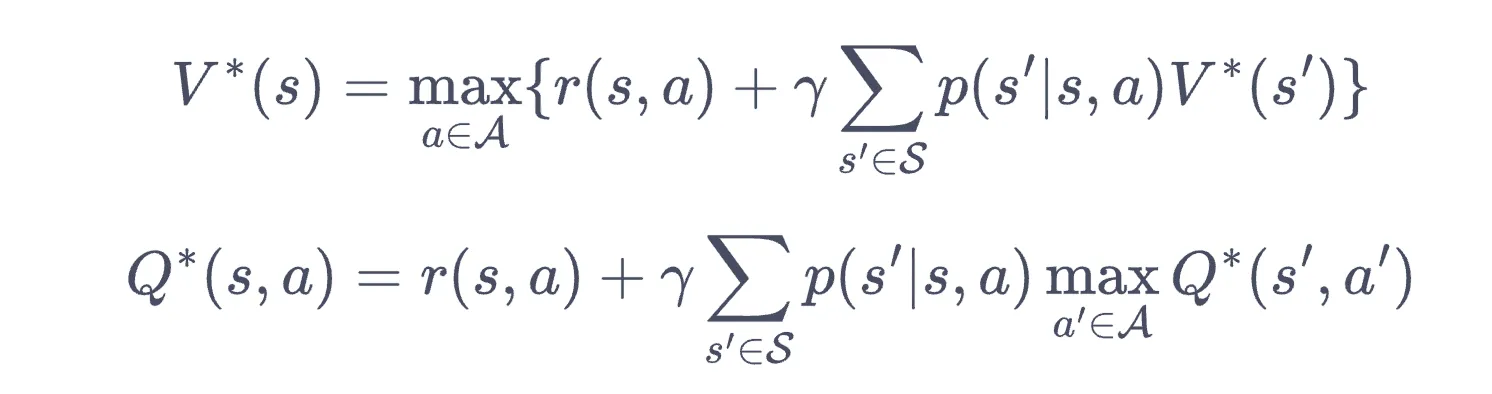-
状态转移矩阵 ,表示状态对转移概率,为方阵,第 行第 个表示 转移到 概率
MRP 问题
- 下方 表示状态集合中的元素, 表示某时刻状态取值
- : 随机变量, 时刻获得的奖励(实际)
- : 转移到状态 s 获得的奖励的期望
- : 随机变量, 时刻获得的奖励
- : 转移到状态 s 获得的奖励的期望******
- : 一个马尔科夫过程中,从状态 开始到无穷步后衰减奖励之和
- : 这里引入了衰减系数,则有
- : 价值函数, 为一个状态的期望回报
- 上一行等号最右边叫做贝尔曼方程,由 V 和邻接 V 组成
- 奖励函数列向量 由 组成
- 贝尔曼方程矩阵形式: 此法复杂度 ,不适用于大数据
MDP 问题
- :动作集合
- :期望奖励同时取决于状态和动作
- :状态转移概率也是,故马尔可夫矩阵不再有用
策略
- :状态 下采取 的概率
- 状态价值函数 state-value function,即还不确定
- 动作价值函数 action-value function,即确定了
- 有
- 有
贝尔曼期望方程
- 代入即可,要么由 V 和邻接 V 组成,要么由 Q 和邻接 Q 组成
- 将 表示为关于下一个状态的等式
- 将 同样表示为关于下一个状态和动作的等式

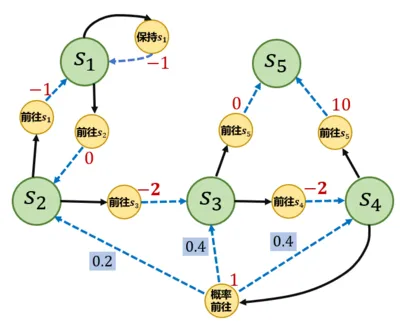
- 和 的例子

边缘化求状态价值函数
- 边缘化:将 MDP 转化为 MRP:状态期望奖励 = 所有动作奖励 动作概率,
蒙特卡洛方法
- 随机采样若干条序列,计算统计回报,用于计算状态价值函数
- , 这是增量更新, 由实际采样计算得到
- 代码实现更新方法:先获得一个序列,对该序列从后往前计算
1def MC(episodes, V, N, gamma):2 # 这里 episode 是一个采样序列3 for episode in episodes:4 G = 05 # 由于 G 的定义跟后续状态有关,只能从后往前计算.6 # 所以最后一个状态没有良好的 G(G = 0)7 for i in range(len(episode) - 1, -1, -1):8 (s, a, r, s_next) = episode[i]9 G = r + gamma * G10 N[s] = N[s] + 111 V[s] = V[s] + (G - V[s]) / N[s]占用度量
- : MDP 的初始状态分布(在状态 的概率)
- : 策略 下智能体 时刻为状态 的概率
- : 状态访问分布, ,指策略下所有步在状态 的概率的衰减加权和
- 似乎需要确定 .
- 性质(离散形式类似于 MDP 贝尔曼期望方程):

- : 占用度量,就是动作状态访问分布,等于状态访问分布乘动作权重,表示策略下所有步在该(状态-动作对)的概率的衰减加权和
- 定理 1: 占用度量相同 策略相同
- 定理 2: 合法占用度量 ,可生成该占用度量的唯一策略为:
最优策略
- 定理:有限状态和动作集合中,必然存在一个策略,在任意状态下的状态价值函数均不劣于其他策略
- 感性上确实能理解
- : …
- 重要:,只需选最好的一个动作即可。这是一个循环依赖,需要解方程
贝尔曼最优方程
- 由上面导出