8 DQN 改进算法

Double DQN

• 上一章的 DQN 在计算 $y^"real"$ 时，使用的是:
• 
• 
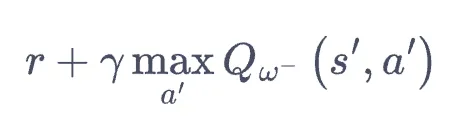
• 如 $w^-$ 有正向误差估计，则 $Q(s, a)$ 会被过高估计，而拿 $Q(s, a)$ 更新上一步 $Q$ 时，误差会逐渐累积。
• 如何解决？将优化目标改为下式，也就是选取下一步最优动作时使用训练网络而不是目标网络. 这样可以缓解此问题.
• 

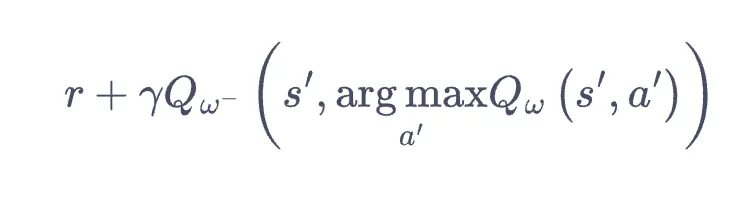
Double DQN 代码区别

        if self.dqn_type == 'DoubleDQN': # DQN与Double DQN的区别
            max_action = self.q_net(next_states).max(1)[1].view(-1, 1)
            max_next_q_values = self.target_q_net(next_states).gather(1, max_action)
        else: # DQN的情况
            max_next_q_values = self.target_q_net(next_states).max(1)[0].view(-1, 1)

结果可视化

打印了两个图.

1. 打印每个 episode 的回报移动平均
2. 对每个时间步，记录该 episode （模拟采样周期）内的移动最大值，这是用于观察是否有 $Q$ 超限的情况

                while not done: # 每个模拟时间步
                    action = agent.take_action(state)
                    max_q_value = agent.max_q_value(
                        state) * 0.005 + max_q_value * 0.995  # 平滑处理
                    max_q_value_list.append(max_q_value)  # 保存每个状态的最大Q值

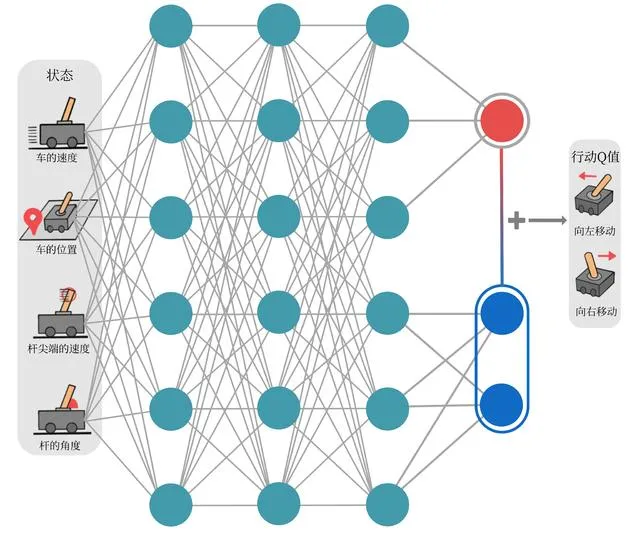
Dueling DQN

• 
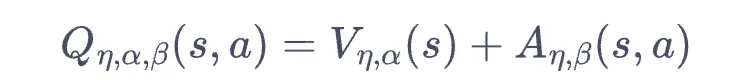
  • 这里 $eta, alpha, beta$ 都是网络参数的意思。
  • $V$ 为状态价值函数，$A$ 为优势函数，数学上定义为 $A(s, a) = Q(s, a) - V(s)$.
• 
• 注意训练数据依然是 $(s, a, r, s^prime)$ 的批量采样.
• 好处：某些情况下动作对价值影响不大。如果分开建模，训练这些情况时注意力会集中在 $V$ 网络上.
• 

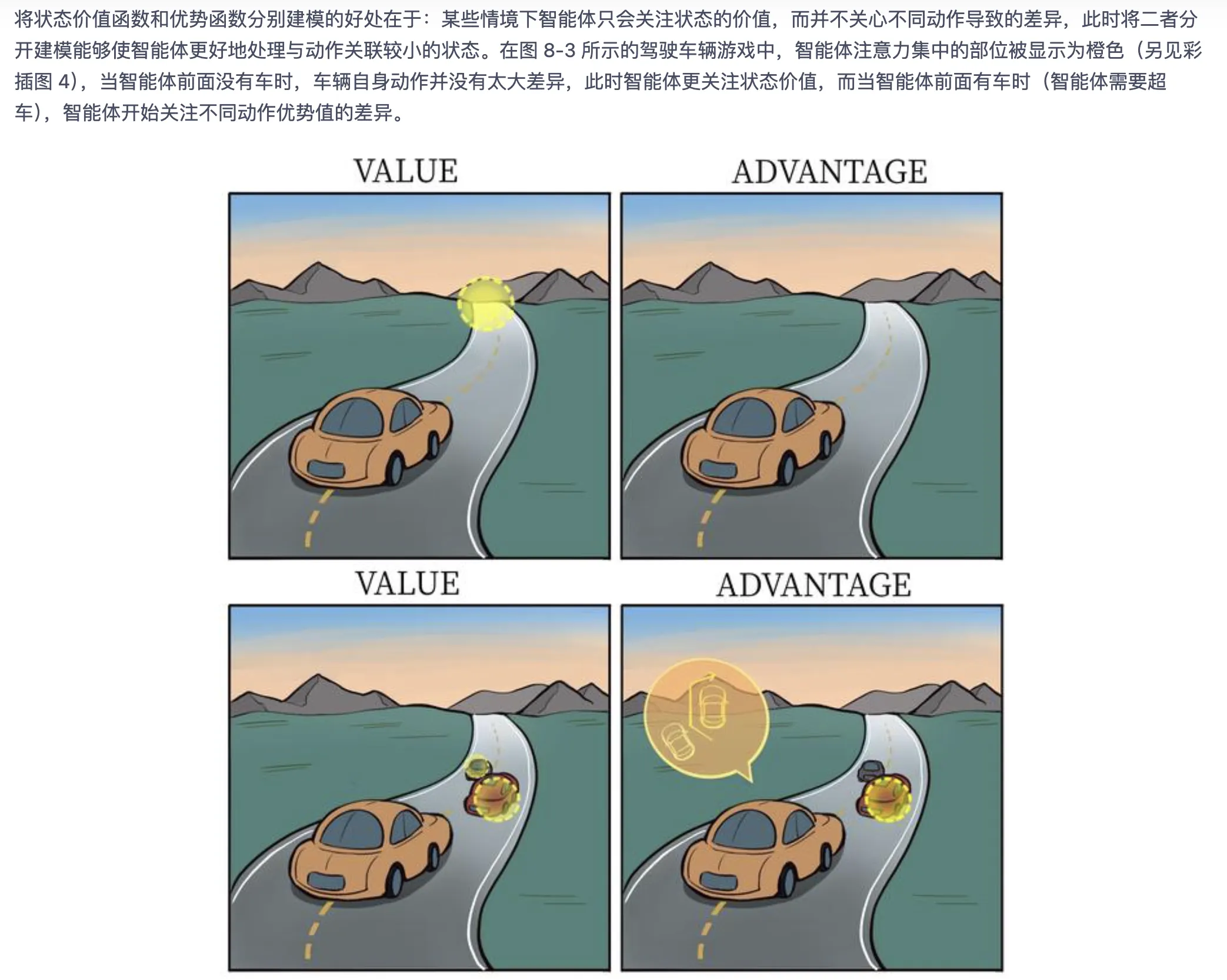
不唯一性问题

• 
• 平均化操作更稳定，训练时采用之.

代码

• 基本上与 DQN 的区别只有下述代码:

class VAnet(torch.nn.Module):
    ''' 只有一层隐藏层的A网络和V网络 '''
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(VAnet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)  # 共享网络部分
        self.fc_A = torch.nn.Linear(hidden_dim, action_dim)
        self.fc_V = torch.nn.Linear(hidden_dim, 1)

    def forward(self, x):
        A = self.fc_A(F.relu(self.fc1(x)))
        V = self.fc_V(F.relu(self.fc1(x)))
        Q = V + A - A.mean(1).view(-1, 1)  # Q值由V值和A值计算得到
        return Q

• 效果 : 学习更加稳定（回报曲线），得到回报的最大值也更优秀.

DQN 对 Q 值过高估计的定量分析

• 利用简单的累积分布函数知识（初中数学知识），如果 Q-net 的 $m$ 个动作的预测值会随机偏大偏小，则预测值的最大值的期望会比真实值最大值大.
  • 当神经网络的预测方差与动作优势值达到同量级时，会非常严重.