9.7.seq2seq
Embedding 层
see: https://blog.csdn.net/zhaohongfei_358/article/details/122809709
与独热编码不同,Embedding 可以将词表降维,且可进行学习。也就是做了 word2vec
import torch
from torch import nn
embedding = nn.Embedding(20, 5)
# 输入必须为 long 类型
embedding(torch.LongTensor([0,1,2]))
# 初始状态为随机编码,会随着梯度下降逐渐学习
tensor([[ 0.4471, 0.3875, -1.0195, -1.1125, 1.3481],
[-1.7230, -0.1964, -0.0420, 0.5782, 0.4514],
[-0.0310, -1.9674, -1.1344, -1.6752, 1.0801]],
grad_fn=<EmbeddingBackward0>)
- 类参数
padding_idx:指定填充的索引,这个索引的向量会被初始化为 0。 - 关于形状:
nl: num_layers,GRU 的隐藏层个数ns: num_steps,时间步- ?
n: batch_size
各层
- Encoder.Embedding 学会将原始语言(en)词元转换为 vec
- Encoder.GRU 学会对 en vec 和上一时刻隐状态给出良好的神秘输出(无意义)和下一时刻 en 隐状态
- Decoder.Embedding 将学会将目标语言(fr)词元转换为 vec
- Decoder.GRU 学会对 fr vec 和上一时刻隐状态给出良好的神秘输出和下一时刻 fr 隐状态
-
Decoder.Dense 学会将神秘输出转换为词元概率
-
Li Mu:
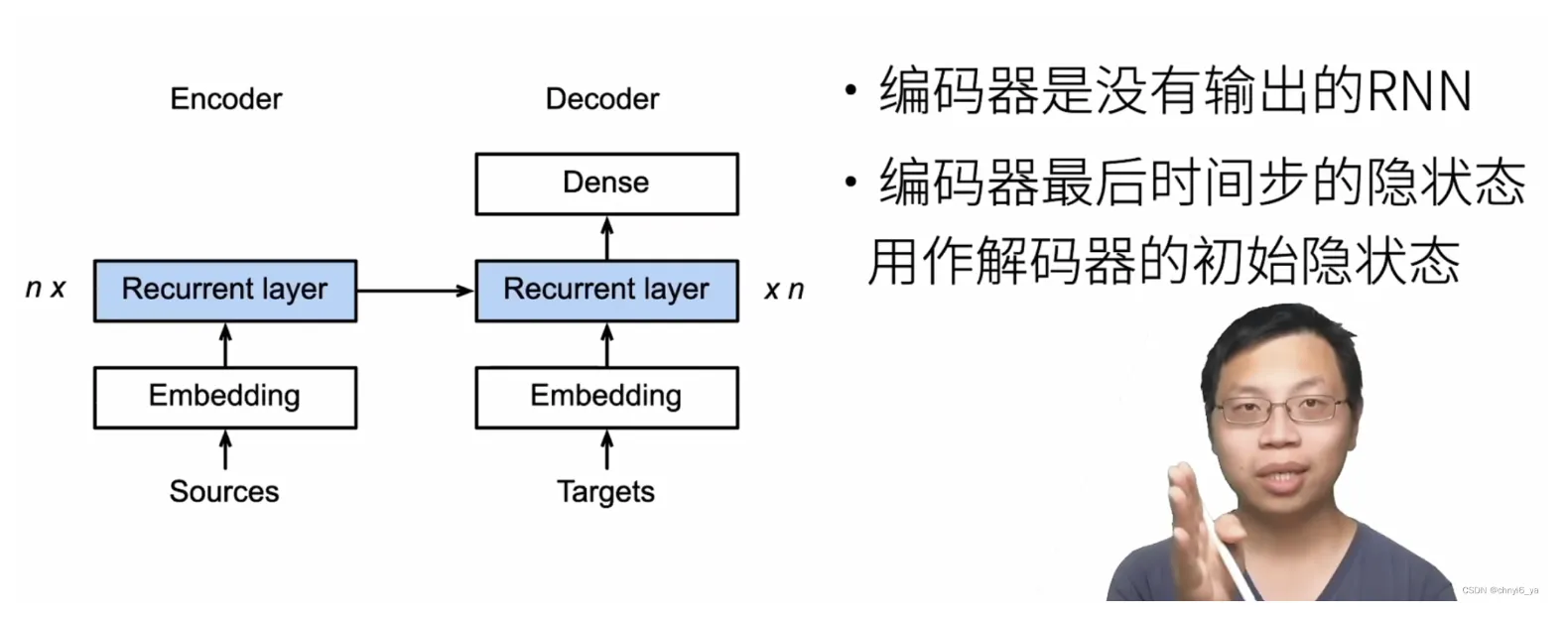
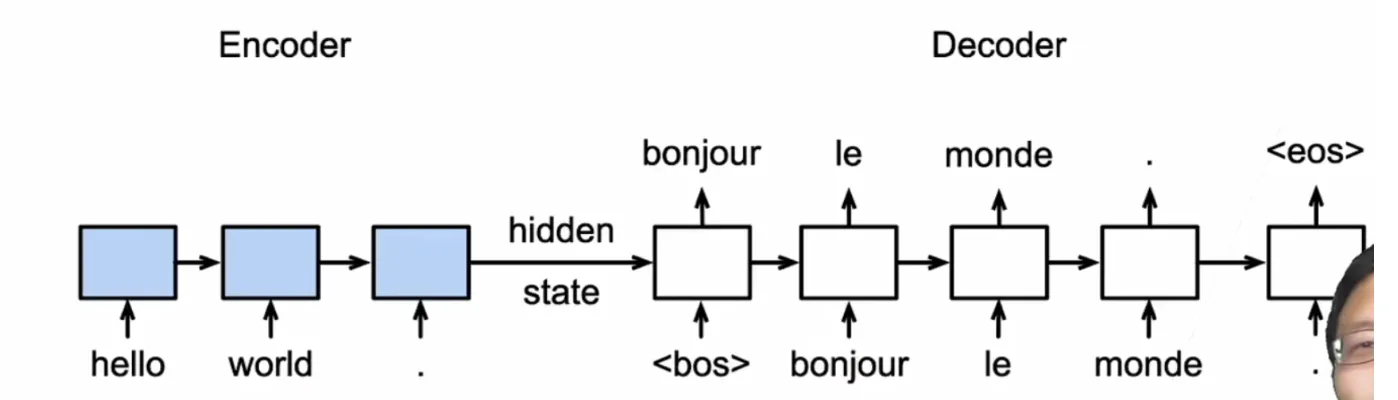
- 训练时 Decoder 输入为正确答案:
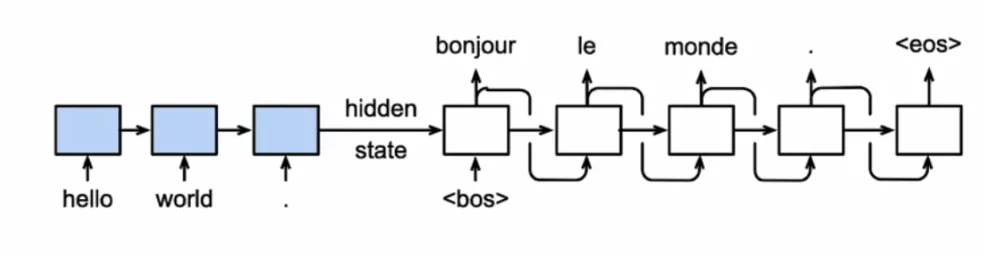
- 推理时 Decoder 输入为上一时刻输出:
外层训练入口
[train]训练时,每对数据仅预测一步,获取损失
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
loss = MaskedSoftmaxCELoss()
for epoch in range(num_epochs):
timer = d2l.Timer()
for batch in data_iter:
optimizer.zero_grad()
X, X_valid_len, Y, Y_valid_len = [x.to(device) for x in batch]
# X 和 Y 的形状:(n, ns)
bos = torch.tensor([tgt_vocab['<bos>']] * Y.shape[0],
device=device).reshape(-1, 1)
# bos 的形状:(n, 1)
dec_input = torch.cat([bos, Y[:, :-1]], 1) # 强制教学
# dec_input 的形状:(n, ns),第一个改为 <bos>
# 强制教学把答案当做输入
# 使 embedding 学会正确编码法语, s.t. GPU 可以正确给出下一时刻的 output + state
# s.t. 使得 Linear 可以根据 output 正确给出词元概率 && 这个 state 可以帮助下一时刻正确给出 output 和 state
# enc_X=X, dec_X=dec_input, *args
Y_hat, _ = net(X, dec_input, X_valid_len)
l = loss(Y_hat, Y, Y_valid_len)
l.sum().backward() # 损失函数的标量进行“反向传播”
d2l.grad_clipping(net, 1)
num_tokens = Y_valid_len.sum()
optimizer.step()
[train.net()]其中enc_X输入为原始语言序列,dec_X输入为目标语言序列答案。
def forward(self, enc_X, dec_X, *args):
enc_outputs = self.encoder(enc_X, *args)
# enc_outputs: (output(ns, n, nh), state(nl, n, nh))
dec_state = self.decoder.init_state(enc_outputs, *args)
# dec_state: 即 state(nl, n, nh)
return self.decoder(dec_X, dec_state)
- 损失函数就是预测出来概率与答案的交叉熵损失. 但是
<pad>需要被排除在外. [train.loss]loss 传入解码器的预测概率(长度为词表大小)和答案序列计算损失,会对valid_len以外的<pad>进行 mask,使之不产生损失。
外层预测入口
- 首先将整个原始句子传入编码器,得到浓缩的所有信息 $bold(c)$
- 传给解码器一步步预测。$bold(c)$ 作为第一步预测的隐状态,接下来每步隐状态会不断更新
# def predict_seq2seq(net, src_sentence, src_vocab, tgt_vocab, num_steps,
# device, save_attention_weights=False):
"""
此处设置解码器网路内部 num_steps = 1,解码器输入的时间长度也为 1,每次只预测一个单词.
"""
src_tokens = src_vocab[src_sentence.lower().split(' ')] + [
src_vocab['<eos>']]
enc_valid_len = torch.tensor([len(src_tokens)], device=device)
src_tokens = d2l.truncate_pad(src_tokens, num_steps, src_vocab['<pad>'])
# 添加批量轴
# 在 shape[0] 处加一维(长度为 1)
# enc_X: shape = (1, len(src_tokens))
enc_X = torch.unsqueeze(
torch.tensor(src_tokens, dtype=torch.long, device=device), dim=0)
# 现将整个 enc_X 传入编码器
# enc_outputs: 包含 output, state
enc_outputs = net.encoder(enc_X, enc_valid_len)
# 此处 [0] output: (ns, n, nh)
# [1] state: (nl, n, nh)
dec_state = net.decoder.init_state(enc_outputs, enc_valid_len)
# dec_state shape: (nl, n, nh) 不包含每个时间步
dec_X = torch.unsqueeze(torch.tensor(
[tgt_vocab['<bos>']], dtype=torch.long, device=device), dim=0)
# dec_X: shape (n, ns) ex (1, 1)
output_seq, attention_weight_seq = [], []
for _ in range(num_steps):
Y, dec_state = net.decoder(dec_X, dec_state)
# Y shape = (1, 1, vocab_size) (n, ns, nvocab)
# 我们使用具有预测最高可能性的词元,作为解码器在下一时间步的输入
dec_X = Y.argmax(dim=2)
pred = dec_X.squeeze(dim=0).type(torch.int32).item()
# 保存注意力权重(稍后讨论)
if save_attention_weights:
attention_weight_seq.append(net.decoder.attention_weights)
# 一旦序列结束词元被预测,输出序列的生成就完成了
if pred == tgt_vocab['<eos>']:
break
output_seq.append(pred)
return ' '.join(tgt_vocab.to_tokens(output_seq)), attention_weight_seq
类
class Seq2SeqEncoder(d2l.Encoder):
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
dropout=0, **kwargs):
super(Seq2SeqEncoder, self).__init__(**kwargs)
# 嵌入层
self.embedding = nn.Embedding(vocab_size, embed_size)
self.rnn = rnn.GRU(num_hiddens, num_layers, dropout=dropout)
def forward(self, X, *args):
# [def] n 是批量
# 输入 X 形状: (n, ns)
X = self.embedding(X)
# 输出'X'的形状:(batch_size,num_steps,embed_size)
# 在循环神经网络模型中,第一个轴对应于时间步
X = X.swapaxes(0, 1)
state = self.rnn.begin_state(batch_size=X.shape[1], ctx=X.ctx)
output, state = self.rnn(X, state)
# output的形状:(num_steps,batch_size,num_hiddens) 被舍弃
# state的形状:(num_layers,batch_size,num_hiddens) 编码全部输入信息
return output, state
class Seq2SeqDecoder(d2l.Decoder):
def __init__(self, vocab_size, embed_size, num_hiddens, num_layers,
dropout=0, **kwargs):
super(Seq2SeqDecoder, self).__init__(**kwargs)
self.embedding = nn.Embedding(vocab_size, embed_size)
self.rnn = nn.GRU(embed_size + num_hiddens, num_hiddens, num_layers,
dropout=dropout)
self.dense = nn.Linear(num_hiddens, vocab_size)
def init_state(self, enc_outputs, *args):
return enc_outputs[1] # 也就是 state
def forward(self, X, state):
# X: shape (n, ns)
# state: shape (nl, n, nh),就是编码器对所有输入信息的编码.
X = self.embedding(X).permute(1, 0, 2)
# X: (ns, n, n_embed) ex (7, 4, 8)
# 此处 state[-1] 是深度循环神经网络最后一层,即最靠近 output 的一层.
# 将这一层复制 n_timestep 次. [这合理吗?]
context = state[-1].repeat(X.shape[0], 1, 1)
# context: (ns, n, nh) ex (7, 4, 16)
X_and_context = torch.cat((X, context), 2)
# X_and_context: (ns, n, n_embed + nh) ex (7, 4, 24)
# 也即,每一时间步每一批量的输入为 n_embed + nh,即 embedding + 刚刚 state 最后一层.
# [qm] 这里 rnn() 怎么又把 state 输入进去了,这不纯信息冗余吗
# 注意 rnn 是一次性循环所有时间步.
output, state = self.rnn(X_and_context, state)
# 此时 output 形状为 (ns, n, nh) 即每时间步每批量输出一个神秘的 nh
output = self.dense(output).permute(1, 0, 2)
# 最终 output的形状:(n, ns, n_vocab) 这里 ns 中的有效长度和输入 X 不同
# state的形状: (num_layers,batch_size,num_hiddens)
return output, state
class EncoderDecoder(nn.Module):
def __init__(self, encoder, decoder, **kwargs):
super(EncoderDecoder, self).__init__(**kwargs)
self.encoder = encoder
self.decoder = decoder
def forward(self, enc_X, dec_X, *args):
enc_outputs = self.encoder(enc_X, *args)
dec_state = self.decoder.init_state(enc_outputs, *args)
return self.decoder(dec_X, dec_state)
手绘流程图
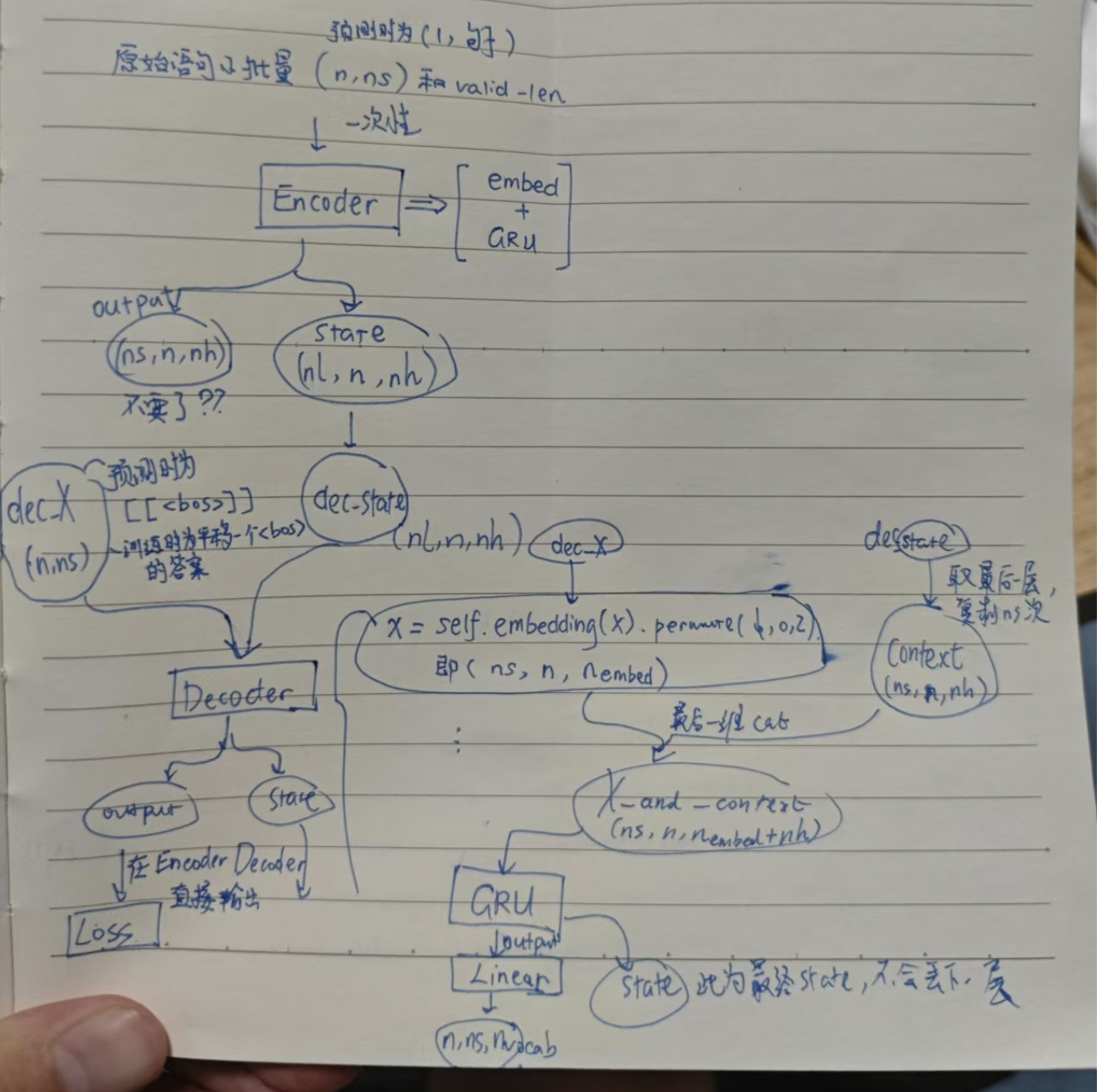
公式
- 解码时隐状态: $$s_(t^prime) = g(y_(t^prime - 1), bold(c), s_(t^prime - 1))$$
- 其中 $c$ 是编码器对整个输入序列 $x_1, ... x_T$ 的编码.
- 这里 $t^prime$ 只是为了和输入序列时间区分.
output, state = self.rnn(X_and_context, state)
output = self.dense(output).permute(1, 0, 2)
BLEU
用于评估预测序列的好坏,值域 $0 tilde 1$。给出预测序列中的 $n$ 元语法有多少出现在标签序列(答案)中。越长的语法权重越大。若预测的太短,会有惩罚。
go . => va !, bleu 1.000
i lost . => j'ai perdu ., bleu 1.000
he's calm . => il est bon ?, bleu 0.537
i'm home . => je suis chez moi debout ., bleu 0.803